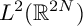 $L^2(\mathbb {R}^{2N})$
$L^2(\mathbb {R}^{2N})$
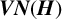 $\boldsymbol {VN(H)}$ AND
$\boldsymbol {VN(H)}$ AND 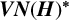 $\boldsymbol {VN(H)^{*}} $ OF AN ULTRASPHERICAL HYPERGROUP
$\boldsymbol {VN(H)^{*}} $ OF AN ULTRASPHERICAL HYPERGROUP 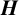 $\boldsymbol {H}$
$\boldsymbol {H}$
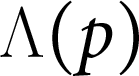 $\Lambda (p)$ Set
$\Lambda (p)$ Set