Refine search
Actions for selected content:
10 results
A note on the column–row property
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1244-1254
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On quotient modules of H2(𝔻n): essential normality and boundary representations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 31 January 2019, pp. 1339-1359
- Print publication:
- June 2020
-
- Article
- Export citation
Fourier Spaces and Completely Isometric Representations of Arens Product Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 717-747
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
EMBEDDINGS AND
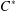 $C^{\ast }$ -ENVELOPES OF EXACT OPERATOR SYSTEMS
$C^{\ast }$ -ENVELOPES OF EXACT OPERATOR SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 274-285
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
A SPECTRAL CHARACTERIZATION OF
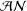 ${\mathcal{A}}{\mathcal{N}}$ OPERATORS
${\mathcal{A}}{\mathcal{N}}$ OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 08 July 2016, pp. 369-391
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
OPERATOR SYSTEM NUCLEARITY VIA
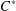 $C^{\ast }$ -ENVELOPES
$C^{\ast }$ -ENVELOPES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 11 May 2016, pp. 356-375
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
THE NON-COMMUTATIVE KHINTCHINE INEQUALITIES FOR
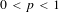 $0<p<1$
$0<p<1$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 5 / November 2017
- Published online by Cambridge University Press:
- 14 October 2015, pp. 1103-1123
- Print publication:
- November 2017
-
- Article
- Export citation
Some Weighted Group Algebras are Operator Algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 05 January 2015, pp. 499-519
-
- Article
-
- You have access
- Export citation
IDEALS IN OPERATOR SPACE PROJECTIVE TENSOR PRODUCT OF C*-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 18 November 2011, pp. 275-288
- Print publication:
- October 2011
-
- Article
-
- You have access
- Export citation
CO-REPRESENTATIONS OF HOPF–VON NEUMANN ALGEBRAS ON OPERATOR SPACES OTHER THAN COLUMN HILBERT SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 22 June 2010, pp. 205-210
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
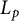



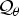
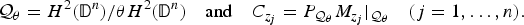

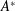

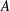
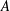
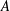
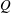
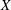
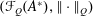
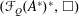
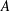


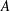
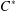




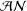
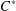
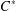
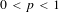
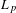
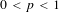
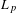
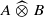 . As an application, a characterization of the prime ideals in the Banach *-algebra
. As an application, a characterization of the prime ideals in the Banach *-algebra 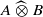 is obtained. In addition, we study the primitive ideals, modular ideals and the maximal modular ideals of
is obtained. In addition, we study the primitive ideals, modular ideals and the maximal modular ideals of 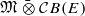 is a Banach algebra if and only if 𝔐 is subhomogeneous or
is a Banach algebra if and only if 𝔐 is subhomogeneous or 