We study convergence rates, in mean, for the Hausdorff metric between a finite set of stationary random variables and their common support, which is supposed to be a compact subset of 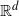$\mathbb{R}^d$. We propose two different approaches for this study. The first is based on the notion of a minimal index. This notion is introduced in this paper. It is in the spirit of the extremal index, which is much used in extreme value theory. The second approach is based on a 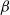$\beta$-mixing condition together with a local-type dependence assumption. More precisely, all our results concern stationary 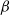$\beta$-mixing sequences satisfying a tail condition, known as the (a, b)-standard assumption, together with a local-type dependence condition or stationary sequences satisfying the (a, b)-standard assumption and having a positive minimal index. We prove that the optimal rates of the independent and identically distributed setting can be reached. We apply our results to stationary Markov chains on a ball, or to a class of Markov chains on a circle or on a torus. We study with simulations the particular examples of a Möbius Markov chain on the unit circle and of a Markov chain on the unit square wrapped on a torus.

Conditions are derived for the asymptotic normality of a general class of vector-valued functionals of stationary Boolean models in the d-dimensional Euclidean space, where a Lindeberg-type central limit theorem for m-dependent random fields, m ∈ N, is applied. These functionals can be used to construct joint estimators for the vector of specific intrinsic volumes of the underlying Boolean model. Extensions to functionals of more general germ–grain models satisfying some mixing and integrability conditions are also discussed.

The germ-grain model is defined as the union of independent identically distributed compact random sets (grains) shifted by points (germs) of a point process. The paper introduces a family of stationary random measures in ℝd generated by germ-grain models and defined by the sum of contributions of non-overlapping parts of the individual grains. The main result of the paper is the central limit theorem for these random measures, which holds for rather general independently marked germ-grain models, including those with non-Poisson distribution of germs and non-convex grains. It is shown that this construction of random measures includes those random measures obtained by positively extended intrinsic volumes. In the Poisson case it is possible to prove a central limit theorem under weaker assumptions by using approximations by m-dependent random fields. Applications to statistics of the Boolean model are also discussed. They include a standard way to derive limit theorems for estimators of the model parameters.