Refine search
Actions for selected content:
22 results
Schwarz lemma for harmonic functions in the unit ball
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 616-633
-
- Article
- Export citation
On the
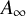 $A_{\infty }$ condition for elliptic operators in 1-sided nontangentially accessible domains satisfying the capacity density condition
$A_{\infty }$ condition for elliptic operators in 1-sided nontangentially accessible domains satisfying the capacity density condition
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 05 August 2022, e59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
UNIQUENESS OF EXTENDABLE TEMPERATURES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 02 October 2020, pp. 311-317
- Print publication:
- April 2021
-
- Article
- Export citation
The Dirichlet Problem for the Slab with Entire Data and a Difference Equation for Harmonic Functions
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 1 / 01 March 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 146-153
- Print publication:
- 01 March 2017
-
- Article
-
- You have access
- Export citation
Quadrature Weights on Tensor-Product Nodes for Accurate Integration of Hypersingular Functions over Some Simple 3-D Geometric Shapes
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 5 / November 2016
- Published online by Cambridge University Press:
- 02 November 2016, pp. 1283-1312
- Print publication:
- November 2016
-
- Article
- Export citation
Fischer Decomposition and Cauchy–Kovalevskaya Extension in Fractional Clifford Analysis: The Riemann–Liouville Case
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 13 June 2016, pp. 251-272
-
- Article
- Export citation
Investigating the Selectivity of KcsA Channel by an Image Charge Solvation Method (ICSM) in Molecular Dynamics Simulations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 12 April 2016, pp. 927-943
- Print publication:
- April 2016
-
- Article
- Export citation
A Well-Conditioned Hypersingular Boundary Element Method for Electrostatic Potentials in the Presence of Inhomogeneities within Layered Media
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 12 April 2016, pp. 970-997
- Print publication:
- April 2016
-
- Article
- Export citation
Heat Kernels and Green Functions on Metric Measure Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 3 / 01 June 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 641-699
- Print publication:
- 01 June 2014
-
- Article
-
- You have access
- Export citation
Random Harmonic Functions in Growth Spaces and Bloch-type Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 2 / 01 April 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 284-302
- Print publication:
- 01 April 2014
-
- Article
-
- You have access
- Export citation
Sharp Inequalities for Differentially Subordinate Harmonic Functions and Martingales
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 3 / 01 September 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 597-610
- Print publication:
- 01 September 2012
-
- Article
-
- You have access
- Export citation
Harmonic morphisms applied to classical potential theory
-
- Journal:
- Nagoya Mathematical Journal / Volume 202 / June 2011
- Published online by Cambridge University Press:
- 11 January 2016, pp. 107-126
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
Image Charge Method for Reaction Fields in a Hybrid Ion-Channel Model
-
- Journal:
- Communications in Computational Physics / Volume 9 / Issue 4 / April 2011
- Published online by Cambridge University Press:
- 20 August 2015, pp. 1056-1070
- Print publication:
- April 2011
-
- Article
- Export citation
A THEOREM OF PHRAGMÉN-LINDELÖF TYPE FOR SUBFUNCTIONS IN A CONE*
-
- Journal:
- Glasgow Mathematical Journal / Volume 53 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 10 March 2011, pp. 599-610
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
POTENTIAL-THEORETIC CHARACTERIZATIONS OF NONSMOOTH DOMAINS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 36 / Issue 4 / July 2004
- Published online by Cambridge University Press:
- 14 June 2004, pp. 469-482
- Print publication:
- July 2004
-
- Article
- Export citation
Toeplitz operators on harmonic Bergman spaces
-
- Journal:
- Nagoya Mathematical Journal / Volume 174 / 2004
- Published online by Cambridge University Press:
- 22 January 2016, pp. 165-186
- Print publication:
- 2004
-
- Article
-
- You have access
- Export citation
Beurling-Dahlberg-Sjögren Type Theorems for Minimally Thin Sets in a Cone
-
- Journal:
- Canadian Mathematical Bulletin / Volume 46 / Issue 2 / 01 June 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 252-264
- Print publication:
- 01 June 2003
-
- Article
-
- You have access
- Export citation
Note on the Support of Sobolev Functions
-
- Journal:
- Canadian Mathematical Bulletin / Volume 41 / Issue 3 / 01 September 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 257-260
- Print publication:
- 01 September 1998
-
- Article
-
- You have access
- Export citation
Subharmonic Extensions and Approximations
-
- Journal:
- Canadian Mathematical Bulletin / Volume 37 / Issue 1 / 01 March 1994
- Published online by Cambridge University Press:
- 20 November 2018, pp. 46-53
- Print publication:
- 01 March 1994
-
- Article
-
- You have access
- Export citation
Two-Weight Norm Inequality and Carleson Measure in Weighted Hardy Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 44 / Issue 6 / 01 December 1992
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1206-1219
- Print publication:
- 01 December 1992
-
- Article
-
- You have access
- Export citation

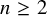
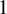

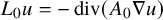
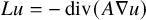

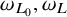
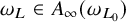
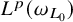
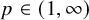
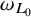
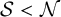
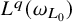
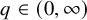
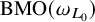
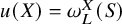
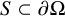
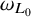
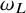
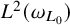
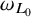
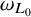
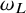
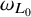
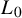
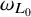
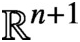
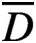
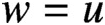
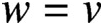
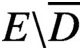
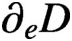
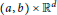

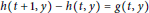
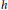
 condition numbers, allowing fast convergence of iterative solvers compared to previous work using first kind of integral equations. We also show that the second order basis converges faster and is more accurate than the first order basis for the BEM.
condition numbers, allowing fast convergence of iterative solvers compared to previous work using first kind of integral equations. We also show that the second order basis converges faster and is more accurate than the first order basis for the BEM.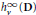
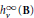
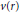

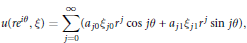
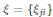
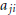

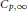
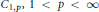
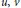


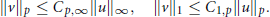
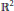

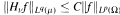 , where
, where 