Let  $\Omega \subset \mathbb {R}^{n+1}$,
$\Omega \subset \mathbb {R}^{n+1}$, 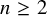 $n\ge 2$, be a
$n\ge 2$, be a 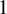 $1$-sided nontangentially accessible domain, that is, a set which is quantitatively open and path-connected. Assume also that
$1$-sided nontangentially accessible domain, that is, a set which is quantitatively open and path-connected. Assume also that  $\Omega $ satisfies the capacity density condition. Let
$\Omega $ satisfies the capacity density condition. Let 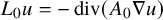 $L_0 u=-\mathop {\operatorname {div}}\nolimits (A_0 \nabla u)$,
$L_0 u=-\mathop {\operatorname {div}}\nolimits (A_0 \nabla u)$, 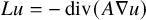 $Lu=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$ be two real (not necessarily symmetric) uniformly elliptic operators in
$Lu=-\mathop {\operatorname {div}}\nolimits (A\nabla u)$ be two real (not necessarily symmetric) uniformly elliptic operators in  $\Omega $, and write
$\Omega $, and write 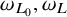 $\omega _{L_0}, \omega _L$ for the respective associated elliptic measures. We establish the equivalence between the following properties: (i)
$\omega _{L_0}, \omega _L$ for the respective associated elliptic measures. We establish the equivalence between the following properties: (i) 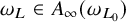 $\omega _L \in A_{\infty }(\omega _{L_0})$, (ii) L is
$\omega _L \in A_{\infty }(\omega _{L_0})$, (ii) L is 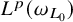 $L^p(\omega _{L_0})$-solvable for some
$L^p(\omega _{L_0})$-solvable for some 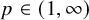 $p\in (1,\infty )$, (iii) bounded null solutions of L satisfy Carleson measure estimates with respect to
$p\in (1,\infty )$, (iii) bounded null solutions of L satisfy Carleson measure estimates with respect to 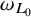 $\omega _{L_0}$, (iv)
$\omega _{L_0}$, (iv) 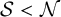 $\mathcal {S}<\mathcal {N}$ (i.e., the conical square function is controlled by the nontangential maximal function) in
$\mathcal {S}<\mathcal {N}$ (i.e., the conical square function is controlled by the nontangential maximal function) in 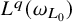 $L^q(\omega _{L_0})$ for some (or for all)
$L^q(\omega _{L_0})$ for some (or for all) 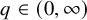 $q\in (0,\infty )$ for any null solution of L, and (v) L is
$q\in (0,\infty )$ for any null solution of L, and (v) L is 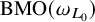 $\mathrm {BMO}(\omega _{L_0})$-solvable. Moreover, in each of the properties (ii)-(v) it is enough to consider the class of solutions given by characteristic functions of Borel sets (i.e,
$\mathrm {BMO}(\omega _{L_0})$-solvable. Moreover, in each of the properties (ii)-(v) it is enough to consider the class of solutions given by characteristic functions of Borel sets (i.e, 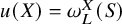 $u(X)=\omega _L^X(S)$ for an arbitrary Borel set
$u(X)=\omega _L^X(S)$ for an arbitrary Borel set 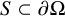 $S\subset \partial \Omega $).
$S\subset \partial \Omega $).
Also, we obtain a qualitative analog of the previous equivalences. Namely, we characterize the absolute continuity of 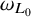 $\omega _{L_0}$ with respect to
$\omega _{L_0}$ with respect to 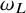 $\omega _L$ in terms of some qualitative local
$\omega _L$ in terms of some qualitative local 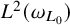 $L^2(\omega _{L_0})$ estimates for the truncated conical square function for any bounded null solution of L. This is also equivalent to the finiteness
$L^2(\omega _{L_0})$ estimates for the truncated conical square function for any bounded null solution of L. This is also equivalent to the finiteness 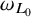 $\omega _{L_0}$-almost everywhere of the truncated conical square function for any bounded null solution of L. As applications, we show that
$\omega _{L_0}$-almost everywhere of the truncated conical square function for any bounded null solution of L. As applications, we show that 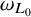 $\omega _{L_0}$ is absolutely continuous with respect to
$\omega _{L_0}$ is absolutely continuous with respect to 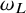 $\omega _L$ if the disagreement of the coefficients satisfies some qualitative quadratic estimate in truncated cones for
$\omega _L$ if the disagreement of the coefficients satisfies some qualitative quadratic estimate in truncated cones for 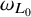 $\omega _{L_0}$-almost everywhere vertex. Finally, when
$\omega _{L_0}$-almost everywhere vertex. Finally, when 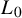 $L_0$ is either the transpose of L or its symmetric part, we obtain the corresponding absolute continuity upon assuming that the antisymmetric part of the coefficients has some controlled oscillation in truncated cones for
$L_0$ is either the transpose of L or its symmetric part, we obtain the corresponding absolute continuity upon assuming that the antisymmetric part of the coefficients has some controlled oscillation in truncated cones for 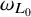 $\omega _{L_0}$-almost every vertex.
$\omega _{L_0}$-almost every vertex.
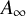 $A_{\infty }$ condition for elliptic operators in 1-sided nontangentially accessible domains satisfying the capacity density condition
$A_{\infty }$ condition for elliptic operators in 1-sided nontangentially accessible domains satisfying the capacity density condition