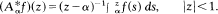Refine search
Actions for selected content:
5 results
A Cesàro-like operator from a class of analytic function spaces to analytic Besov spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1210-1222
- Print publication:
- December 2025
-
- Article
- Export citation
Isomorphic Structure of Cesàro and Tandori Spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 501-532
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Corrigendum to “Generalized Cesàro Matrices”
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 1 / 01 March 2017
- Published online by Cambridge University Press:
- 20 November 2018, p. 196
- Print publication:
- 01 March 2017
-
- Article
-
- You have access
- Export citation
SPECTRUM AND COMPACTNESS OF THE CESÀRO OPERATOR ON WEIGHTED
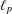 $\ell _{p}$ SPACES
$\ell _{p}$ SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 19 August 2015, pp. 287-314
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Generalized Cesàro Matrices
-
- Journal:
- Canadian Mathematical Bulletin / Volume 27 / Issue 4 / 01 December 1984
- Published online by Cambridge University Press:
- 20 November 2018, pp. 417-422
- Print publication:
- 01 December 1984
-
- Article
-
- You have access
- Export citation

















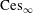
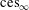
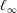
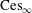
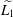
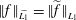
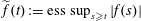
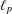
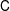
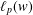
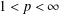
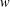
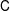
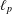

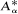 is the operator formally defined on the Hardy space
is the operator formally defined on the Hardy space