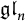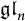In this article, we consider the categorical symmetric Howe duality introduced by Khovanov, Lauda, Sussan, and Yonezawa. While originally defined from a purely diagrammatic perspective, this construction also has geometric and representation-theoretic interpretations, corresponding to certain perverse sheaves on spaces of quiver representations and the category of Gelfand–Tsetlin modules over 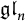$\mathfrak {gl}_n$. In particular, we show that the “deformed Webster algebras” discussed in [KLSY18] manifest a Koszul duality between blocks of the category of Gelfand–Tsetlin modules over 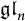$\mathfrak {gl}_n$, and the constructible sheaves on representations of a linear quiver invariant under a certain parabolic in the group that acts by changing bases. Furthermore, we show that this duality intertwines translation functors with a diagrammatic categorical action (generalizing that of [KLSY18]).

We study a dual pair of general linear Lie superalgebras in the sense of R. Howe. We give an explicit multiplicity-free decomposition of a symmetric and skew-symmetric algebra (in the super sense) under the action of the dual pair and present explicit formulas for the highest-weight vectors in each isotypic subspace of the symmetric algebra. We give an explicit multiplicity-free decomposition into irreducible gl(m|n)-modules of the symmetric and skew-symmetric algebras of the symmetric square of the natural representation of gl(m|n). In the former case, we also find explicit formulas for the highest-weight vectors. Our work unifies and generalizes the classical results in symmetric and skew-symmetric models and admits several applications.