We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The lattice walks in the plane starting at the origin 
$\mathbf {0}$ with steps in 
$\{-1,0,1\}^{2}\setminus \{\mathbf {0}\}$ are called king walks. We investigate enumeration and divisibility for higher dimensional king walks confined to certain regions. Specifically, we establish an explicit formula for the number of 
$(r+s)$-dimensional king walks of length n ending at 
$(a_1,\ldots ,a_r,b_1,\ldots ,b_s)$ which never dip below 
$x_i=0$ for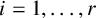 
$i=1,\ldots ,r$. We also derive divisibility properties for the number of 
$(r+s)$-dimensional king walks of length p (an odd prime) through group actions.
Let Mn and Tn denote the nth Motzkin number and the nth central trinomial coefficient respectively. We prove that for any prime 
$p\ge 5$,
\begin{equation*}\begin{aligned}\\[-22pt]&\sum_{k=0}^{p-1}M_k^2\equiv \left(\frac{p}{3}\right)\left(2-6p\right)\pmod{p^2},\\&\sum_{k=0}^{p-1}kM_k^2\equiv \left(\frac{p}{3}\right)\left(9p-1\right)\pmod{p^2},\\&\sum_{k=0}^{p-1}T_kM_k\equiv \frac{4}{3}\left(\frac{p}{3}\right)+\frac{p}{6}\left(1-9\left(\frac{p}{3}\right)\right)\pmod{p^2},\\[-6pt]\end{aligned}\end{equation*}
where 
$\left(-\right)$ is the Legendre symbol. These results confirm three supercongruences conjectured by Z.-W. Sun in 2010.
