Refine search
Actions for selected content:
27 results
ON ASYMPTOTIC PROPERTIES OF NONLINEAR FUNCTIONALS OF RANDOM FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 05 September 2022, pp. 518-521
- Print publication:
- December 2022
-
- Article
-
- You have access
- HTML
- Export citation
On the modified Palm version
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue A / December 2018
- Published online by Cambridge University Press:
- 01 February 2019, pp. 271-280
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Overly determined agents prevent consensus in a generalized Deffuant model on ℤ with dispersed opinions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 September 2017, pp. 722-744
- Print publication:
- September 2017
-
- Article
- Export citation
On long-range dependence of random measures
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 11 January 2017, pp. 1235-1255
- Print publication:
- December 2016
-
- Article
- Export citation
What is typical?
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue A / August 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 379-389
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
Directionally convex ordering of random measures, shot noise fields, and some applications to wireless communications
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 623-646
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Some distributional results for Poisson-Voronoi tessellations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 16-40
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Renewal of singularity sets of random self-similar measures
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 162-188
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
A class of self-similar random measure
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 908-914
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
Fully coupled FBSDE with Brownian motion and Poisson process in stopping time duration
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 2 / April 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 249-266
- Print publication:
- April 2003
-
- Article
-
- You have access
- Export citation
A family of densities derived from the three-parameter Dirichlet process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 39 / Issue 4 / December 2002
- Published online by Cambridge University Press:
- 14 July 2016, pp. 764-774
- Print publication:
- December 2002
-
- Article
- Export citation
Generalized contact distributions of inhomogeneous Boolean models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 1 / March 2002
- Published online by Cambridge University Press:
- 19 February 2016, pp. 21-47
- Print publication:
- March 2002
-
- Article
- Export citation
Random fractals and probability metrics
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 925-947
- Print publication:
- December 2000
-
- Article
- Export citation
Generalized Gamma measures and shot-noise Cox processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 929-953
- Print publication:
- December 1999
-
- Article
- Export citation
Central limit theorem for a class of random measures associated with germ-grain models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 283-314
- Print publication:
- June 1999
-
- Article
- Export citation
On the distribution of the spherical contact vector of stationary germ-grain models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 30 / Issue 1 / March 1998
- Published online by Cambridge University Press:
- 01 July 2016, pp. 36-52
- Print publication:
- March 1998
-
- Article
- Export citation
Linear Programming Estimators and Bootstrapping for Heavy Tailed Phenomena
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 29 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 01 July 2016, pp. 759-805
- Print publication:
- September 1997
-
- Article
- Export citation
Heavy traffic analysis for continuous polling models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 3 / September 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 720-732
- Print publication:
- September 1997
-
- Article
- Export citation
A flow conservation law for surface processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 13-28
- Print publication:
- March 1996
-
- Article
- Export citation
Note on generalizations of Mecke's formula and extensions of H = λG
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 105-122
- Print publication:
- March 1995
-
- Article
- Export citation
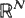 and
and 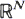 . The pair is jointly stationary, i.e. its distribution is invariant under translations. The vector field
. The pair is jointly stationary, i.e. its distribution is invariant under translations. The vector field 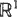 this specializes to a well-known rate conservation law for point processes. As an application, relationships for the linear contact distribution of Φ are derived.
this specializes to a well-known rate conservation law for point processes. As an application, relationships for the linear contact distribution of Φ are derived.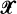 , and relates integrations concerning them to each other. For
, and relates integrations concerning them to each other. For 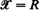 , we generalize this to a pair of random measures which are jointly stationary. The resulting formula extends the so-called Swiss Army formula, which was recently obtained as a generalization for Little's formula. The generalized Mecke formula, which is called GMF, can be also viewed as a generalization of the stationary version of
, we generalize this to a pair of random measures which are jointly stationary. The resulting formula extends the so-called Swiss Army formula, which was recently obtained as a generalization for Little's formula. The generalized Mecke formula, which is called GMF, can be also viewed as a generalization of the stationary version of 