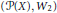Refine search
Actions for selected content:
2 results
Isometric rigidity of the Wasserstein space over the plane with the maximum metric
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 June 2025, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
First Variation Formula in Wasserstein Spaces over Compact Alexandrov Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 4 / 01 December 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 723-735
- Print publication:
- 01 December 2012
-
- Article
-
- You have access
- Export citation