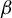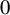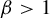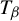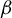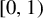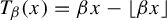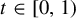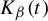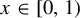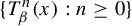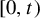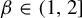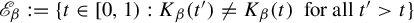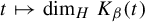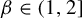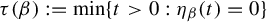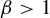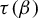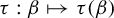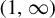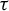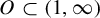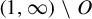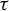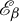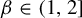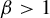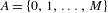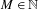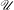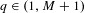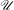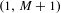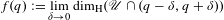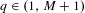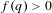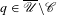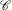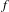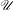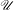Given 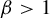 $\beta>1$, let
$\beta>1$, let 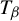 $T_\beta $ be the
$T_\beta $ be the 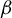 $\beta $-transformation on the unit circle
$\beta $-transformation on the unit circle 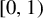 $[0,1)$, defined by
$[0,1)$, defined by 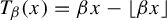 $T_\beta (x)=\beta x-\lfloor \beta x\rfloor $. For each
$T_\beta (x)=\beta x-\lfloor \beta x\rfloor $. For each 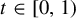 $t\in [0,1)$, let
$t\in [0,1)$, let 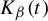 $K_\beta (t)$ be the survivor set consisting of all
$K_\beta (t)$ be the survivor set consisting of all 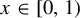 $x\in [0,1)$ whose orbit
$x\in [0,1)$ whose orbit 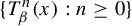 $\{T^n_\beta (x): n\ge 0\}$ never enters the interval
$\{T^n_\beta (x): n\ge 0\}$ never enters the interval 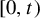 $[0,t)$. Kalle et al [Ergod. Th. & Dynam. Sys. 40(9) (2020), 2482–2514] considered the case
$[0,t)$. Kalle et al [Ergod. Th. & Dynam. Sys. 40(9) (2020), 2482–2514] considered the case 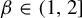 $\beta \in (1,2]$. They studied the set-valued bifurcation set
$\beta \in (1,2]$. They studied the set-valued bifurcation set 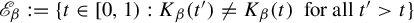 $\mathscr {E}_\beta :=\{t\in [0,1): K_\beta (t')\ne K_\beta (t)~\text { for all } t'>t\}$ and proved that the Hausdorff dimension function
$\mathscr {E}_\beta :=\{t\in [0,1): K_\beta (t')\ne K_\beta (t)~\text { for all } t'>t\}$ and proved that the Hausdorff dimension function 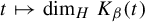 $t\mapsto \dim _H K_\beta (t)$ is a non-increasing Devil’s staircase. In a previous paper [Ergod. Th. & Dynam. Sys. 43(6) (2023), 1785–1828], we determined, for all
$t\mapsto \dim _H K_\beta (t)$ is a non-increasing Devil’s staircase. In a previous paper [Ergod. Th. & Dynam. Sys. 43(6) (2023), 1785–1828], we determined, for all 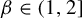 $\beta \in (1,2]$, the critical value
$\beta \in (1,2]$, the critical value 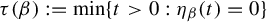 $\tau (\beta ):=\min \{t>0: \eta _\beta (t)=0\}$. The purpose of the present article is to extend these results to all
$\tau (\beta ):=\min \{t>0: \eta _\beta (t)=0\}$. The purpose of the present article is to extend these results to all 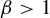 $\beta>1$. In addition to calculating
$\beta>1$. In addition to calculating 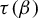 $\tau (\beta )$, we show that: (i) the function
$\tau (\beta )$, we show that: (i) the function 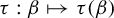 $\tau : \beta \mapsto \tau (\beta )$ is left-continuous on
$\tau : \beta \mapsto \tau (\beta )$ is left-continuous on 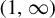 $(1,\infty )$ with right-hand limits everywhere, but has countably infinitely many discontinuities; (ii)
$(1,\infty )$ with right-hand limits everywhere, but has countably infinitely many discontinuities; (ii) 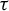 $\tau $ has no downward jumps; and (iii) there exists an open set
$\tau $ has no downward jumps; and (iii) there exists an open set 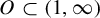 $O\subset (1,\infty )$, whose complement
$O\subset (1,\infty )$, whose complement 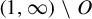 $(1,\infty )\setminus O$ has zero Hausdorff dimension, such that
$(1,\infty )\setminus O$ has zero Hausdorff dimension, such that 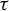 $\tau $ is real-analytic, strictly convex, and strictly decreasing on each connected component of O. We also prove several topological properties of the bifurcation set
$\tau $ is real-analytic, strictly convex, and strictly decreasing on each connected component of O. We also prove several topological properties of the bifurcation set 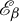 $\mathscr {E}_\beta $. The key to extending the results from
$\mathscr {E}_\beta $. The key to extending the results from 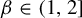 $\beta \in (1,2]$ to all
$\beta \in (1,2]$ to all 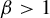 $\beta>1$ is an appropriate generalization of the Farey words that are used to parameterize the connected components of the set O. Some of the original proofs from the above-mentioned papers are simplified.
$\beta>1$ is an appropriate generalization of the Farey words that are used to parameterize the connected components of the set O. Some of the original proofs from the above-mentioned papers are simplified.
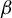 $\beta $-transformation with a hole at
$\beta $-transformation with a hole at 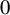 $0$: the general case
$0$: the general case