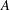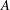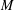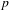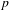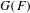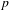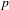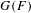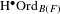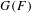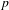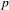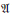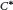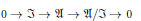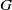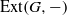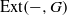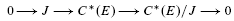Refine search
Actions for selected content:
9 results
16 - Basic Galois theory
- from Part II - Extensions and applications
-
- Book:
- Modular Forms and String Theory
- Published online:
- 28 November 2024
- Print publication:
- 12 December 2024, pp 332-344
-
- Chapter
- Export citation
UNIVERSISM AND EXTENSIONS OF V
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 21 July 2020, pp. 112-154
- Print publication:
- March 2021
-
- Article
- Export citation
On Extensions for Gentle Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 28 January 2020, pp. 249-292
- Print publication:
- February 2021
-
- Article
- Export citation
EXT-FINITE MODULES FOR WEAKLY SYMMETRIC ALGEBRAS WITH RADICAL CUBE ZERO
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 108-121
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
EXTENSIONS ENTRE SÉRIES PRINCIPALES
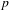 $p$-ADIQUES ET MODULO
$p$-ADIQUES ET MODULO 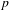 $p$ DE
$p$ DE 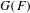 $G(F)$
$G(F)$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 08 August 2014, pp. 225-270
- Print publication:
- April 2016
-
- Article
- Export citation
The Ordered K-theory of a Full Extension
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 3 / 01 June 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 596-624
- Print publication:
- 01 June 2014
-
- Article
-
- You have access
- Export citation
COMMUTING PROPERTIES OF EXT
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 25 February 2013, pp. 276-288
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
Index maps in the K-theory of graph algebras
-
- Journal:
- Journal of K-Theory / Volume 9 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 17 May 2011, pp. 385-406
- Print publication:
- April 2012
-
- Article
- Export citation
Essentially commutative C*-algebras with essential spectrum homeomorphic to S2n−1
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 2 / April 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 199-210
- Print publication:
- April 2001
-
- Article
-
- You have access
- Export citation