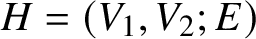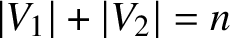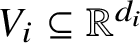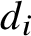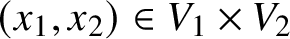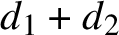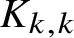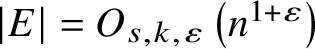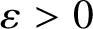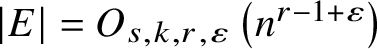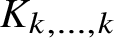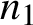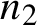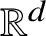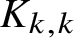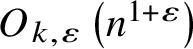A bipartite graph 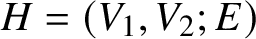$H = \left (V_1, V_2; E \right )$ with 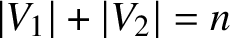$\lvert V_1\rvert + \lvert V_2\rvert = n$ is semilinear if 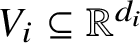$V_i \subseteq \mathbb {R}^{d_i}$ for some 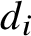$d_i$ and the edge relation E consists of the pairs of points 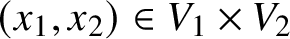$(x_1, x_2) \in V_1 \times V_2$ satisfying a fixed Boolean combination of s linear equalities and inequalities in 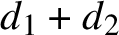$d_1 + d_2$ variables for some s. We show that for a fixed k, the number of edges in a 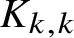$K_{k,k}$-free semilinear H is almost linear in n, namely 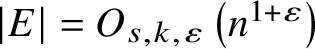$\lvert E\rvert = O_{s,k,\varepsilon }\left (n^{1+\varepsilon }\right )$ for any 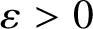$\varepsilon> 0$; and more generally, 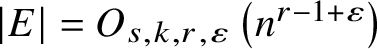$\lvert E\rvert = O_{s,k,r,\varepsilon }\left (n^{r-1 + \varepsilon }\right )$ for a 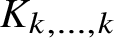$K_{k, \dotsc ,k}$-free semilinear r-partite r-uniform hypergraph.

As an application, we obtain the following incidence bound: given 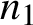$n_1$ points and 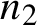$n_2$ open boxes with axis-parallel sides in 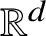$\mathbb {R}^d$ such that their incidence graph is 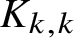$K_{k,k}$-free, there can be at most 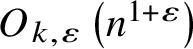$O_{k,\varepsilon }\left (n^{1+\varepsilon }\right )$ incidences. The same bound holds if instead of boxes, one takes polytopes cut out by the translates of an arbitrary fixed finite set of half-spaces.

We also obtain matching upper and (superlinear) lower bounds in the case of dyadic boxes on the plane, and point out some connections to the model-theoretic trichotomy in o-minimal structures (showing that the failure of an almost-linear bound for some definable graph allows one to recover the field operations from that graph in a definable manner).

In this paper we deal with the model theory of differentially closed fields of characteristic zero with finitely many commuting derivations. First we observe that the only known lower bound for the Lascar rank of types in differentially closed fields, announced in a paper of McGrail, is false. This gives us a new class of regular types which are orthogonal to fields. Then we classify the subgroups of the additive group of Lascar rank omega with differential-type 1 which are nonorthogonal to fields. The last parts consist of an analysis of the quotients of the heat variety. We show that the generic type of such a quotient is locally modular. Finally, we answer a question of Phylliss Cassidy about the existence of certain Jordan-Hölder type series in the negative.