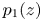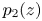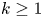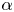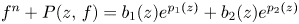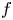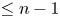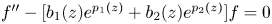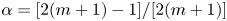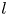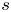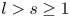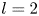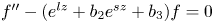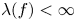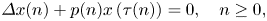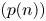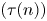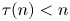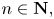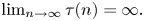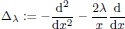Refine search
Actions for selected content:
37 results
7 - Cell Differentiation through Development
-
- Book:
- Universal Biology
- Published online:
- 11 November 2025
- Print publication:
- 20 November 2025, pp 181-215
-
- Chapter
- Export citation
3 - Oscillation and Excitability in Cellular Dynamics
-
- Book:
- Theoretical Biology of the Cell
- Published online:
- 05 June 2025
- Print publication:
- 19 June 2025, pp 72-96
-
- Chapter
- Export citation

Theoretical Biology of the Cell
- A Dynamical-Systems Perspective
-
- Published online:
- 05 June 2025
- Print publication:
- 19 June 2025
Chapter 15 - Neuronal Activity in the Basal Ganglia and Thalamus in Patients with Parkinson’s Disease
- from Section 2: - Hypokinetic Movement Disorders
-
-
- Book:
- International Compendium of Movement Disorders
- Published online:
- 07 January 2025
- Print publication:
- 06 February 2025, pp 181-193
-
- Chapter
- Export citation
6 - Introductory Dynamics
-
- Book:
- Quantum Models of Cognition and Decision
- Published online:
- 14 November 2024
- Print publication:
- 21 November 2024, pp 178-209
-
- Chapter
- Export citation
8 - Oscillations and CP Violation in Quarks
-
- Book:
- Introduction to Elementary Particle Physics
- Published online:
- 08 November 2024
- Print publication:
- 27 June 2024, pp 315-350
-
- Chapter
-
- You have access
- Open access
- HTML
- Export citation
Experimental studies on the Hartmann tube
-
- Journal:
- The Aeronautical Journal / Volume 128 / Issue 1328 / October 2024
- Published online by Cambridge University Press:
- 11 April 2024, pp. 2281-2307
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exploring Damping Properties of IRIS Bright Points using Deep Learning Techniques
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 19 / Issue S365 / December 2023
- Published online by Cambridge University Press:
- 23 December 2024, pp. 399-403
- Print publication:
- December 2023
-
- Article
- Export citation
5 - Extreme Sensescapes
- from Part II - Responses and Restitutions
-
- Book:
- Sensory Anthropology
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp 124-160
-
- Chapter
- Export citation
On the oscillation of certain second-order linear differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 09 December 2022, pp. 1965-1992
- Print publication:
- December 2023
-
- Article
- Export citation
Upper and lower limit oscillation conditions for first-order difference equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 07 July 2022, pp. 618-631
-
- Article
- Export citation
OSCILLATION OF IMPULSIVE LINEAR DIFFERENTIAL EQUATIONS WITH DISCONTINUOUS SOLUTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 05 May 2022, pp. 112-124
- Print publication:
- February 2023
-
- Article
- Export citation
BEYOND SLOW-FAST: RELAXATION OSCILLATIONS IN SINGULARLY PERTURBED NONSMOOTH SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 10 June 2021, pp. 342-343
- Print publication:
- October 2021
-
- Article
-
- You have access
- Export citation
Chapter Two - Mathematical Description of Oscillations
-
- Book:
- Ocean Waves and Oscillating Systems
- Published online:
- 12 May 2020
- Print publication:
- 28 May 2020, pp 6-45
-
- Chapter
- Export citation
Chapter One - Introduction
-
- Book:
- Ocean Waves and Oscillating Systems
- Published online:
- 12 May 2020
- Print publication:
- 28 May 2020, pp 1-5
-
- Chapter
- Export citation
Chapter Six - Oscillating-Body Wave-Energy Converters
-
- Book:
- Ocean Waves and Oscillating Systems
- Published online:
- 12 May 2020
- Print publication:
- 28 May 2020, pp 204-241
-
- Chapter
- Export citation

Ocean Waves and Oscillating Systems
- Linear Interactions Including Wave-Energy Extraction
-
- Published online:
- 12 May 2020
- Print publication:
- 28 May 2020
Weibel instability oscillation in a dusty plasma with counter-streaming electrons
-
- Journal:
- Laser and Particle Beams / Volume 38 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 17 January 2020, pp. 8-13
-
- Article
- Export citation
Oscillation Criteria for Second Order Ordinary Differential Equations
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 13 September 2019, pp. 276-286
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Oscillation and variation for the Riesz transform associated with Bessel operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 18 September 2018, pp. 169-190
- Print publication:
- February 2019
-
- Article
- Export citation