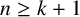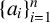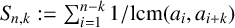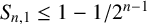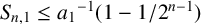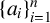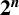Refine search
Actions for selected content:
8 results
Reciprocal associations between parental depression and child cognition: Pathways to children’s internalizing and externalizing symptoms
-
- Journal:
- Development and Psychopathology / Volume 37 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 06 November 2023, pp. 29-39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Within-person pathways among maternal depressive symptoms and offspring internalizing problems from early childhood through adolescence
-
- Journal:
- Development and Psychopathology / Volume 36 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1145-1153
-
- Article
- Export citation
13 - Becoming a Strategic Reader
- from Part III - Developing Reading Comprehension Abilities
-
- Book:
- Reading in a Second Language
- Published online:
- 01 September 2022
- Print publication:
- 08 September 2022, pp 312-337
-
- Chapter
- Export citation
7 - Event Structure and Nonprototypical Argument Coding
- from Part III - Clause Structure
-
- Book:
- Morphosyntax
- Published online:
- 04 August 2022
- Print publication:
- 04 August 2022, pp 206-244
-
- Chapter
- Export citation
A SHARP UPPER BOUND FOR THE SUM OF RECIPROCALS OF LEAST COMMON MULTIPLES II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 09 June 2022, pp. 10-21
- Print publication:
- February 2023
-
- Article
- Export citation
RECIPROCAL MONOGENIC QUINTINOMIALS OF DEGREE
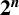 $\boldsymbol {2^n}$
$\boldsymbol {2^n}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 04 March 2022, pp. 437-447
- Print publication:
- December 2022
-
- Article
- Export citation
2 - Indigenous Historic Trade in the Western Hemisphere
- from Part I - Indigenous Peoples and International Trade and Investment
-
-
- Book:
- Indigenous Peoples and International Trade
- Published online:
- 11 June 2020
- Print publication:
- 18 June 2020, pp 43-66
-
- Chapter
- Export citation