Refine search
Actions for selected content:
13 results
Integrable dispersive generalisation of Ovsyannikov two-layer shallow water model
-
- Journal:
- Journal of Nonlinear Waves / Volume 1 / 2025
- Published online by Cambridge University Press:
- 09 December 2025, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A mathematical analysis of the Kakinuma model for interfacial gravity waves. Part II: justification as a shallow water approximation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 18 March 2024, pp. 2049-2120
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Caulleryaspis chicosciencei: a new species from Brazil (Annelida, Sternaspidae)
-
- Journal:
- Journal of the Marine Biological Association of the United Kingdom / Volume 102 / Issue 6 / September 2022
- Published online by Cambridge University Press:
- 12 September 2022, pp. 402-407
-
- Article
- Export citation
ON THE TOPOGRAPHY-DRIVEN VORTICITY PRODUCTION IN SHALLOW LAKES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 03 May 2019, pp. 148-160
-
- Article
-
- You have access
- Export citation
Giving up on elaborate dermal ossicles: a new genus of ossicleless Apodida (Holothuroidea)
-
- Journal:
- Journal of the Marine Biological Association of the United Kingdom / Volume 98 / Issue 7 / November 2018
- Published online by Cambridge University Press:
- 30 June 2017, pp. 1685-1688
-
- Article
- Export citation
Morphodynamics of a storm-dominated, shallow tidal inlet: the Slufter, the Netherlands
-
- Journal:
- Netherlands Journal of Geosciences / Volume 91 / Issue 3 / November 2012
- Published online by Cambridge University Press:
- 24 March 2014, pp. 325-339
-
- Article
-
- You have access
- Export citation
Boundary Conditions for Limited Area Models Based on the Shallow Water Equations
-
- Journal:
- Communications in Computational Physics / Volume 14 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 03 June 2015, pp. 664-702
- Print publication:
- September 2013
-
- Article
- Export citation
Formal derivation of a bilayer model coupling shallow water and Reynolds lubrication equations: evolution of a thin pollutant layer over water
-
- Journal:
- European Journal of Applied Mathematics / Volume 24 / Issue 6 / December 2013
- Published online by Cambridge University Press:
- 27 June 2013, pp. 803-833
-
- Article
- Export citation
Robust a Simulation for Shallow Flows with Friction on Rough Topography
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 6 / Issue 2 / May 2013
- Published online by Cambridge University Press:
- 28 May 2015, pp. 384-407
- Print publication:
- May 2013
-
- Article
- Export citation
The propagation of high-Reynolds-number non-Boussinesq gravity currents in axisymmetric geometry
-
- Journal:
- Journal of Fluid Mechanics / Volume 643 / 25 January 2010
- Published online by Cambridge University Press:
- 24 December 2009, pp. 267-277
-
- Article
- Export citation
Population changes and reproduction of an alien spionid polychaete, Streblospio gynobranchiata, in shallow waters of the south Caspian Sea
-
- Journal:
- Marine Biodiversity Records / Volume 2 / January 2009
- Published online by Cambridge University Press:
- 03 March 2009, e40
- Print publication:
- January 2009
-
- Article
- Export citation
An entropy-correction free solver for non-homogeneous shallow water equations
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 37 / Issue 5 / September 2003
- Published online by Cambridge University Press:
- 15 November 2003, pp. 755-772
- Print publication:
- September 2003
-
- Article
- Export citation
On the two-dimensional compressible isentropic Navier–Stokes equations
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 36 / Issue 6 / November 2002
- Published online by Cambridge University Press:
- 15 January 2003, pp. 1091-1109
- Print publication:
- November 2002
-
- Article
- Export citation




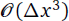 . The method is applied to solve problems with complex rough topography, coupled with
. The method is applied to solve problems with complex rough topography, coupled with