We discuss a continuous-time Markov branching model in which each individual can trigger an alarm according to a Poisson process. The model is stopped when a given number of alarms is triggered or when there are no more individuals present. Our goal is to determine the distribution of the state of the population at this stopping time. In addition, the state distribution at any fixed time is also obtained. The model is then modified to take into account the possible influence of death cases. All distributions are derived using probability-generating functions, and the approach followed is based on the construction of families of martingales.

Let ξ0,ξ1,ξ2,… be a homogeneous Markov process and let S n denote the partial sum S n = θ(ξ1) + … + θ(ξn ), where θ(ξ) is a scalar nonlinearity. If N is a stopping time with 𝔼N < ∞ and the Markov process satisfies certain ergodicity properties, we then show that 𝔼S N = [limn→∞𝔼θ(ξn )]𝔼N + 𝔼ω(ξ0) − 𝔼ω(ξN ). The function ω(ξ) is a well defined scalar nonlinearity directly related to θ(ξ) through a Poisson integral equation, with the characteristic that ω(ξ) becomes zero in the i.i.d. case. Consequently our result constitutes an extension to Wald's first lemma for the case of Markov processes. We also show that, when 𝔼N → ∞, the correction term is negligible as compared to 𝔼N in the sense that 𝔼ω(ξ0) − 𝔼ω(ξN ) = o(𝔼N).

Kallenberg [2] introduced the concept of F-exchangeable sequences of random variables and produced some characterizations of F-exchangeability in terms of stopping times. In this paper ways of extending the concept of F-exchangeability to doubly indexed arrays of random variables are explored and some characterizations obtained for row and column exchangebale arrays, weakly exchangeable arrays and separately exchangeable continuous processes.

Let X 1 , X 2 , · ··, Xn be positive i.i.d. random variables with known distribution function having a finite mean. For a given s ≥0 we define Nn = N(n, s) to be the largest number k such that the sum of the smallest k Xs does not exceed s, and Mn = M(n, s) to be the largest number k such that the sum of the largest k X's does not exceed s. This paper studies the precise and asymptotic behaviour of E(Nn ), E(Mn ), Nn, Mn, and the corresponding ‘stopped' order statistics 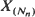and 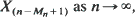as n →∞, both for fixed s, and where s =sn is an increasing function of n.

The problem of finding optimal replacement strategies for certain classes of failure systems is considered. These systems can be repaired upon failure, but are stochastically deteriorating, i.e., the lengths of the operating intervals decrease in some sense, whereas the durations of the repairs increase. For several models of this type optimal replacement strategies are derived under natural assumptions on the reward and the cost structure.

Two Wiener-Hopf type factorization identities for multivariate distributions are introduced. Properties of associated stopping times are derived. The structure that produces one factorization also provides the unique solution of the Wiener-Hopf convolution equation on a convex cone in R d . Some applications for multivariate storage and queueing systems are indicated. For a few cases explicit formulas are obtained for the transforms of the associated stopping times. A result of Kemperman is extended.

An occupation measure describes the expected amount of time a stochastic process spends in different parts of its state space prior to a given random time. It is shown that a basic identity involving occupation measures provides a unified approach to a variety of moment identities for Markov chains, and some connections with potential theory are made.

Some Wiener-Hopf type results are collected, related and given more direct proofs. Spitzer's random-walk method for the Wiener-Hopf integral equation also produces his factorisation relating functionals of maxima and minima. Transform equations are interpreted as decompositions of time-changed processes. Discrete- and continuous-time versions are related. Prabhu's factorisation for generators is equivalent to Fristedt's Lévy measure factorisation and to process decomposition.