Refine search
Actions for selected content:
2 results
Shared dynamically small points for polynomials on average
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 46 / Issue 2 / February 2026
- Published online by Cambridge University Press:
- 01 September 2025, pp. 373-416
- Print publication:
- February 2026
-
- Article
- Export citation
Some unlikely intersections beyond André–Oort
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 30 August 2011, pp. 1-27
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation





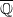 . Finally, we formulate and prove a variant of the Mordell–Lang conjecture for subvarieties of
. Finally, we formulate and prove a variant of the Mordell–Lang conjecture for subvarieties of 