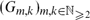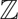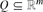Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
13 - Tractability and Modern Satisfiability Modulo Theories Solvers
- from Part 5 - Heuristics
-
-
- Book:
- Tractability
- Published online:
- 05 February 2014
- Print publication:
- 06 February 2014, pp 350-377
-
- Chapter
- Export citation
Part 5 - Heuristics
-
- Book:
- Tractability
- Published online:
- 05 February 2014
- Print publication:
- 06 February 2014, pp 329-330
-
- Chapter
- Export citation
Part 1 - Graphical Structure
-
- Book:
- Tractability
- Published online:
- 05 February 2014
- Print publication:
- 06 February 2014, pp 1-2
-
- Chapter
- Export citation
Contributors
-
- Book:
- Tractability
- Published online:
- 05 February 2014
- Print publication:
- 06 February 2014, pp xi-xii
-
- Chapter
- Export citation
6 - Tree-Reweighted Message Passing
- from Part 3 - Algorithms and their Analysis
-
-
- Book:
- Tractability
- Published online:
- 05 February 2014
- Print publication:
- 06 February 2014, pp 175-201
-
- Chapter
- Export citation
Contents
-
- Book:
- Tractability
- Published online:
- 05 February 2014
- Print publication:
- 06 February 2014, pp v-x
-
- Chapter
- Export citation
10 - Efficient Submodular Function Minimization for Computer Vision
- from Part 4 - Tractability in Some Specific Areas
-
-
- Book:
- Tractability
- Published online:
- 05 February 2014
- Print publication:
- 06 February 2014, pp 285-303
-
- Chapter
- Export citation
Part 2 - Language Restrictions
-
- Book:
- Tractability
- Published online:
- 05 February 2014
- Print publication:
- 06 February 2014, pp 69-70
-
- Chapter
- Export citation
5 - Tractable Knowledge Representation Formalisms
- from Part 2 - Language Restrictions
-
-
- Book:
- Tractability
- Published online:
- 05 February 2014
- Print publication:
- 06 February 2014, pp 141-172
-
- Chapter
- Export citation
9 - Kernelization Methods for Fixed-Parameter Tractability
- from Part 3 - Algorithms and their Analysis
-
-
- Book:
- Tractability
- Published online:
- 05 February 2014
- Print publication:
- 06 February 2014, pp 260-282
-
- Chapter
- Export citation
Introduction
-
-
- Book:
- Tractability
- Published online:
- 05 February 2014
- Print publication:
- 06 February 2014, pp xiii-xxii
-
- Chapter
- Export citation

Tractability
- Practical Approaches to Hard Problems
-
- Published online:
- 05 February 2014
- Print publication:
- 06 February 2014
On the Diameters of Commuting Graphs Arising from Random Skew-Symmetric Matrices
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 3 / May 2014
- Published online by Cambridge University Press:
- 04 February 2014, pp. 449-459
-
- Article
- Export citation
One-Rule Length-Preserving Rewrite Systems and RationalTransductions
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 48 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 21 January 2014, pp. 149-171
- Print publication:
- April 2014
-
- Article
- Export citation
Incremental DFA minimisation∗
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 48 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 21 January 2014, pp. 173-186
- Print publication:
- April 2014
-
- Article
- Export citation
On the Importance Sampling of Self-Avoiding Walks
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 5 / September 2014
- Published online by Cambridge University Press:
- 20 January 2014, pp. 725-748
-
- Article
- Export citation
Invariant Measure Under the Affine Group Over
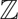 ${\mathbb{Z}$
${\mathbb{Z}$
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 2 / March 2014
- Published online by Cambridge University Press:
- 02 January 2014, pp. 248-268
-
- Article
- Export citation
Reaction automata working in sequential manner∗∗∗
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 48 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 21 January 2014, pp. 23-38
- Print publication:
- January 2014
-
- Article
- Export citation
Systems of parallel communicating restartingautomata
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 48 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 21 January 2014, pp. 3-22
- Print publication:
- January 2014
-
- Article
- Export citation
Transducing by observing length-reducing and painterrules
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 48 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 10 February 2014, pp. 85-105
- Print publication:
- January 2014
-
- Article
- Export citation