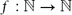Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
A Generalized Model of PAC Learning and itsApplicability
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 48 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 09 April 2014, pp. 209-245
- Print publication:
- April 2014
-
- Article
- Export citation
Colouring Planar Graphs With Three Colours and No Large Monochromatic Components
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 4 / July 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 551-570
-
- Article
- Export citation
New Bounds for Edge-Cover by Random Walk
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 4 / July 2014
- Published online by Cambridge University Press:
- 11 March 2014, pp. 571-584
-
- Article
- Export citation
Robust Analysis of Preferential Attachment Models with Fitness
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 3 / May 2014
- Published online by Cambridge University Press:
- 24 February 2014, pp. 386-411
-
- Article
- Export citation
CPC volume 23 issue 2 Cover and Back matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 2 / March 2014
- Published online by Cambridge University Press:
- 19 February 2014, pp. b1-b7
-
- Article
-
- You have access
- Export citation
CPC volume 23 issue 2 Cover and Front matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 2 / March 2014
- Published online by Cambridge University Press:
- 19 February 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Partially Observed Boolean Sequences and Noise Sensitivity
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 3 / May 2014
- Published online by Cambridge University Press:
- 13 February 2014, pp. 317-330
-
- Article
- Export citation
The Asymptotic Number of Connected d-Uniform Hypergraphs†
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 3 / May 2014
- Published online by Cambridge University Press:
- 13 February 2014, pp. 367-385
-
- Article
- Export citation
Local Limit Theorems for the Giant Component of Random Hypergraphs†
-
- Journal:
- Combinatorics, Probability and Computing / Volume 23 / Issue 3 / May 2014
- Published online by Cambridge University Press:
- 13 February 2014, pp. 331-366
-
- Article
- Export citation
2 - Perfect Graphs and Graphical Modeling
- from Part 1 - Graphical Structure
-
-
- Book:
- Tractability
- Published online:
- 05 February 2014
- Print publication:
- 06 February 2014, pp 39-68
-
- Chapter
- Export citation
1 - Treewidth and Hypertree Width
- from Part 1 - Graphical Structure
-
-
- Book:
- Tractability
- Published online:
- 05 February 2014
- Print publication:
- 06 February 2014, pp 3-38
-
- Chapter
- Export citation
Part 3 - Algorithms and their Analysis
-
- Book:
- Tractability
- Published online:
- 05 February 2014
- Print publication:
- 06 February 2014, pp 173-174
-
- Chapter
- Export citation
7 - Tractable Optimization in Machine Learning
- from Part 3 - Algorithms and their Analysis
-
-
- Book:
- Tractability
- Published online:
- 05 February 2014
- Print publication:
- 06 February 2014, pp 202-230
-
- Chapter
- Export citation
8 - Approximation Algorithms
- from Part 3 - Algorithms and their Analysis
-
-
- Book:
- Tractability
- Published online:
- 05 February 2014
- Print publication:
- 06 February 2014, pp 231-259
-
- Chapter
- Export citation
3 - Submodular Function Maximization
- from Part 2 - Language Restrictions
-
-
- Book:
- Tractability
- Published online:
- 05 February 2014
- Print publication:
- 06 February 2014, pp 71-104
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Tractability
- Published online:
- 05 February 2014
- Print publication:
- 06 February 2014, pp i-iv
-
- Chapter
- Export citation
11 - Towards Practical Graph-Based, Iteratively Decoded Channel Codes: Insights through Absorbing Sets
- from Part 4 - Tractability in Some Specific Areas
-
-
- Book:
- Tractability
- Published online:
- 05 February 2014
- Print publication:
- 06 February 2014, pp 304-328
-
- Chapter
- Export citation
12 - SAT Solvers
- from Part 5 - Heuristics
-
-
- Book:
- Tractability
- Published online:
- 05 February 2014
- Print publication:
- 06 February 2014, pp 331-349
-
- Chapter
- Export citation
4 - Tractable Valued Constraints
- from Part 2 - Language Restrictions
-
-
- Book:
- Tractability
- Published online:
- 05 February 2014
- Print publication:
- 06 February 2014, pp 105-140
-
- Chapter
- Export citation
Part 4 - Tractability in Some Specific Areas
-
- Book:
- Tractability
- Published online:
- 05 February 2014
- Print publication:
- 06 February 2014, pp 283-284
-
- Chapter
- Export citation