Refine search
Actions for selected content:
6975 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
Standard factors of Sturmian words
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 February 2010, pp. 159-174
- Print publication:
- January 2010
-
- Article
- Export citation
Formal language propertiesof hybrid systems with strong resets
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 February 2010, pp. 79-111
- Print publication:
- January 2010
-
- Article
- Export citation
How to build billiard wordsusing decimations
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 February 2010, pp. 59-77
- Print publication:
- January 2010
-
- Article
- Export citation
Foreword
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 February 2010, p. 1
- Print publication:
- January 2010
-
- Article
- Export citation
On the computation of covert channel capacity
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 February 2010, pp. 37-58
- Print publication:
- January 2010
-
- Article
- Export citation
Morphisms fixing words associatedwith exchange of three intervals
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 February 2010, pp. 3-17
- Print publication:
- January 2010
-
- Article
- Export citation
The critical exponent of the Arshon words
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 February 2010, pp. 139-150
- Print publication:
- January 2010
-
- Article
- Export citation
Infinite words containing squaresat every position
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 February 2010, pp. 113-124
- Print publication:
- January 2010
-
- Article
- Export citation
On the growth rates of complexity of threshold languages
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 February 2010, pp. 175-192
- Print publication:
- January 2010
-
- Article
- Export citation
Radix enumeration of rational languages
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 February 2010, pp. 19-36
- Print publication:
- January 2010
-
- Article
- Export citation
Binary words avoiding the pattern AABBCABBA
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 February 2010, pp. 151-158
- Print publication:
- January 2010
-
- Article
- Export citation
Tight Bounds for Blind Search on the Integers and the Reals
-
- Journal:
- Combinatorics, Probability and Computing / Volume 19 / Issue 5-6 / November 2010
- Published online by Cambridge University Press:
- 18 December 2009, pp. 711-728
-
- Article
- Export citation
9 - Timing
-
- Book:
- Process Algebra: Equational Theories of Communicating Processes
- Published online:
- 05 July 2014
- Print publication:
- 16 December 2009, pp 301-334
-
- Chapter
- Export citation
Preface
-
- Book:
- Process Algebra: Equational Theories of Communicating Processes
- Published online:
- 05 July 2014
- Print publication:
- 16 December 2009, pp xiii-xvi
-
- Chapter
- Export citation
Index of Authors
-
- Book:
- Process Algebra: Equational Theories of Communicating Processes
- Published online:
- 05 July 2014
- Print publication:
- 16 December 2009, pp 435-438
-
- Chapter
- Export citation
7 - Parallel and communicating processes
-
- Book:
- Process Algebra: Equational Theories of Communicating Processes
- Published online:
- 05 July 2014
- Print publication:
- 16 December 2009, pp 195-244
-
- Chapter
- Export citation
12 - Semantics
-
- Book:
- Process Algebra: Equational Theories of Communicating Processes
- Published online:
- 05 July 2014
- Print publication:
- 16 December 2009, pp 393-410
-
- Chapter
- Export citation
3 - Transition systems
-
- Book:
- Process Algebra: Equational Theories of Communicating Processes
- Published online:
- 05 July 2014
- Print publication:
- 16 December 2009, pp 35-66
-
- Chapter
- Export citation
2 - Preliminaries
-
- Book:
- Process Algebra: Equational Theories of Communicating Processes
- Published online:
- 05 July 2014
- Print publication:
- 16 December 2009, pp 11-34
-
- Chapter
- Export citation
Foreword
-
-
- Book:
- Process Algebra: Equational Theories of Communicating Processes
- Published online:
- 05 July 2014
- Print publication:
- 16 December 2009, pp x-xi
-
- Chapter
- Export citation
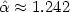
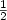
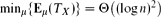 . The same bounds are proved for the analogous continuous process, where step sizes and token positions are real values in [0,
. The same bounds are proved for the analogous continuous process, where step sizes and token positions are real values in [0, 