Refine search
Actions for selected content:
6975 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
CPC volume 19 issue 2 Cover and Back matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 19 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 05 February 2010, pp. b1-b2
-
- Article
-
- You have access
- Export citation
WDM and Directed Star Arboricity
-
- Journal:
- Combinatorics, Probability and Computing / Volume 19 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 05 February 2010, pp. 161-182
-
- Article
- Export citation
CPC volume 19 issue 2 Cover and Front matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 19 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 05 February 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation

A First Course in Combinatorial Optimization
-
- Published online:
- 28 January 2010
- Print publication:
- 09 February 2004

A Unifying Framework for Structured Analysis and Design Models
- An Approach Using Initial Algebra Semantics and Category Theory
-
- Published online:
- 28 January 2010
- Print publication:
- 09 May 1991

Theories of Programming Languages
-
- Published online:
- 28 January 2010
- Print publication:
- 13 October 1998
Area Limit Laws for Symmetry Classes of Staircase Polygons
-
- Journal:
- Combinatorics, Probability and Computing / Volume 19 / Issue 3 / May 2010
- Published online by Cambridge University Press:
- 27 January 2010, pp. 441-461
-
- Article
- Export citation
On the syntactic complexity of tree series
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 26 January 2010, pp. 257-279
- Print publication:
- April 2010
-
- Article
- Export citation
Extending regular expressionswith homomorphic replacement
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 26 January 2010, pp. 229-255
- Print publication:
- April 2010
-
- Article
- Export citation
CHAPTER I - INTRODUCTION
-
- Book:
- Logical Foundations of Proof Complexity
- Published online:
- 06 July 2010
- Print publication:
- 25 January 2010, pp 1-8
-
- Chapter
- Export citation
APPENDIX A - COMPUTATION MODELS
-
- Book:
- Logical Foundations of Proof Complexity
- Published online:
- 06 July 2010
- Print publication:
- 25 January 2010, pp 445-456
-
- Chapter
- Export citation
CHAPTER II - THE PREDICATE CALCULUS AND THE SYSTEM LK
-
- Book:
- Logical Foundations of Proof Complexity
- Published online:
- 06 July 2010
- Print publication:
- 25 January 2010, pp 9-38
-
- Chapter
- Export citation
CHAPTER VI - THE THEORY V1 AND POLYNOMIAL TIME
-
- Book:
- Logical Foundations of Proof Complexity
- Published online:
- 06 July 2010
- Print publication:
- 25 January 2010, pp 133-158
-
- Chapter
- Export citation
CHAPTER III - PEANO ARITHMETIC AND ITS SUBSYSTEMS
-
- Book:
- Logical Foundations of Proof Complexity
- Published online:
- 06 July 2010
- Print publication:
- 25 January 2010, pp 39-72
-
- Chapter
- Export citation
CHAPTER VIII - THEORIES FOR POLYNOMIAL TIME AND BEYOND
-
- Book:
- Logical Foundations of Proof Complexity
- Published online:
- 06 July 2010
- Print publication:
- 25 January 2010, pp 201-266
-
- Chapter
- Export citation
CHAPTER IV - TWO-SORTED LOGIC AND COMPLEXITY CLASSES
-
- Book:
- Logical Foundations of Proof Complexity
- Published online:
- 06 July 2010
- Print publication:
- 25 January 2010, pp 73-94
-
- Chapter
- Export citation
PREFACE
-
- Book:
- Logical Foundations of Proof Complexity
- Published online:
- 06 July 2010
- Print publication:
- 25 January 2010, pp xiii-xvi
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Logical Foundations of Proof Complexity
- Published online:
- 06 July 2010
- Print publication:
- 25 January 2010, pp i-vi
-
- Chapter
- Export citation
BIBLIOGRAPHY
-
- Book:
- Logical Foundations of Proof Complexity
- Published online:
- 06 July 2010
- Print publication:
- 25 January 2010, pp 457-464
-
- Chapter
- Export citation
CHAPTER VII - PROPOSITIONAL TRANSLATIONS
-
- Book:
- Logical Foundations of Proof Complexity
- Published online:
- 06 July 2010
- Print publication:
- 25 January 2010, pp 159-200
-
- Chapter
- Export citation
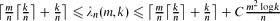 for some constant
for some constant 