Refine search
Actions for selected content:
6975 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
CHAPTER IX - THEORIES FOR SMALL CLASSES
-
- Book:
- Logical Foundations of Proof Complexity
- Published online:
- 06 July 2010
- Print publication:
- 25 January 2010, pp 267-362
-
- Chapter
- Export citation
Contents
-
- Book:
- Logical Foundations of Proof Complexity
- Published online:
- 06 July 2010
- Print publication:
- 25 January 2010, pp vii-xii
-
- Chapter
- Export citation
CHAPTER X - PROOF SYSTEMS AND THE REFLECTION PRINCIPLE
-
- Book:
- Logical Foundations of Proof Complexity
- Published online:
- 06 July 2010
- Print publication:
- 25 January 2010, pp 363-444
-
- Chapter
- Export citation
CHAPTER V - THE THEORY V0 AND AC0
-
- Book:
- Logical Foundations of Proof Complexity
- Published online:
- 06 July 2010
- Print publication:
- 25 January 2010, pp 95-132
-
- Chapter
- Export citation
INDEX
-
- Book:
- Logical Foundations of Proof Complexity
- Published online:
- 06 July 2010
- Print publication:
- 25 January 2010, pp 465-479
-
- Chapter
- Export citation
Sumset and Inverse Sumset Theory for Shannon Entropy
-
- Journal:
- Combinatorics, Probability and Computing / Volume 19 / Issue 4 / July 2010
- Published online by Cambridge University Press:
- 22 January 2010, pp. 603-639
-
- Article
- Export citation
On the Subtree Size Profile of Binary Search trees
-
- Journal:
- Combinatorics, Probability and Computing / Volume 19 / Issue 4 / July 2010
- Published online by Cambridge University Press:
- 22 January 2010, pp. 561-578
-
- Article
- Export citation

Higher Order Logic and Hardware Verification
-
- Published online:
- 21 January 2010
- Print publication:
- 11 November 1993

Action Semantics
-
- Published online:
- 19 January 2010
- Print publication:
- 13 August 1992

Lectures in Logic and Set Theory
-
- Published online:
- 16 January 2010
- Print publication:
- 09 January 2003

The Geometry of Information Retrieval
-
- Published online:
- 14 January 2010
- Print publication:
- 12 August 2004

Efficient Algorithms for Listing Combinatorial Structures
-
- Published online:
- 14 January 2010
- Print publication:
- 22 April 1993

Noisy Information and Computational Complexity
-
- Published online:
- 13 January 2010
- Print publication:
- 16 May 1996

Evolution and Structure of the Internet
- A Statistical Physics Approach
-
- Published online:
- 12 January 2010
- Print publication:
- 12 February 2004

The Clausal Theory of Types
-
- Published online:
- 12 January 2010
- Print publication:
- 22 April 1993

Lectures in Logic and Set Theory
-
- Published online:
- 12 January 2010
- Print publication:
- 13 February 2003

Process Algebra
-
- Published online:
- 08 January 2010
- Print publication:
- 25 October 1990

Predicate Transformer Semantics
-
- Published online:
- 06 January 2010
- Print publication:
- 13 August 1992

Nets, Terms and Formulas
- Three Views of Concurrent Processes and their Relationship
-
- Published online:
- 06 January 2010
- Print publication:
- 03 October 1991
On the number of squares in partial words
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 11 February 2010, pp. 125-138
- Print publication:
- January 2010
-
- Article
- Export citation
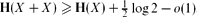 , where
, where 