Refine search
Actions for selected content:
6975 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
A survey of simple permutations
-
-
- Book:
- Permutation Patterns
- Published online:
- 05 October 2010
- Print publication:
- 03 June 2010, pp 41-66
-
- Chapter
- Export citation
The lexicographic first occurrence of a I-II-III-pattern
-
-
- Book:
- Permutation Patterns
- Published online:
- 05 October 2010
- Print publication:
- 03 June 2010, pp 213-220
-
- Chapter
- Export citation
Contents
-
- Book:
- Permutation Patterns
- Published online:
- 05 October 2010
- Print publication:
- 03 June 2010, pp v-vi
-
- Chapter
- Export citation
Combinatorial properties of permutation tableaux
-
-
- Book:
- Permutation Patterns
- Published online:
- 05 October 2010
- Print publication:
- 03 June 2010, pp 171-192
-
- Chapter
- Export citation
Preface
-
- Book:
- Permutation Patterns
- Published online:
- 05 October 2010
- Print publication:
- 03 June 2010, pp vii-viii
-
- Chapter
- Export citation
On the permutational power of token passing networks
-
-
- Book:
- Permutation Patterns
- Published online:
- 05 October 2010
- Print publication:
- 03 June 2010, pp 317-338
-
- Chapter
- Export citation
On three different notions of monotone subsequences
-
-
- Book:
- Permutation Patterns
- Published online:
- 05 October 2010
- Print publication:
- 03 June 2010, pp 89-114
-
- Chapter
- Export citation
Enumeration schemes for words avoiding permutations
-
-
- Book:
- Permutation Patterns
- Published online:
- 05 October 2010
- Print publication:
- 03 June 2010, pp 193-212
-
- Chapter
- Export citation
Restricted patience sorting and barred pattern avoidance
-
-
- Book:
- Permutation Patterns
- Published online:
- 05 October 2010
- Print publication:
- 03 June 2010, pp 233-258
-
- Chapter
- Export citation
Permutations with k-regular descent patterns
-
-
- Book:
- Permutation Patterns
- Published online:
- 05 October 2010
- Print publication:
- 03 June 2010, pp 259-286
-
- Chapter
- Export citation
CPC volume 19 issue 4 Cover and Back matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 19 / Issue 4 / July 2010
- Published online by Cambridge University Press:
- 28 May 2010, pp. b1-b3
-
- Article
-
- You have access
- Export citation
CPC volume 19 issue 4 Cover and Front matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 19 / Issue 4 / July 2010
- Published online by Cambridge University Press:
- 28 May 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation

Designing Economic Mechanisms
-
- Published online:
- 24 May 2010
- Print publication:
- 22 May 2006
An Improved Bound for k-Sets in Four Dimensions
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 20 May 2010, pp. 119-129
-
- Article
- Export citation

Linear Logic in Computer Science
-
- Published online:
- 17 May 2010
- Print publication:
- 15 November 2004

Models and Computability
-
- Published online:
- 17 May 2010
- Print publication:
- 17 June 1999
Sub-Gaussian Tails for the Number of Triangles in G(n, p)
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 14 May 2010, pp. 155-160
-
- Article
- Export citation
Exit Frequency Matrices for Finite Markov Chains
-
- Journal:
- Combinatorics, Probability and Computing / Volume 19 / Issue 4 / July 2010
- Published online by Cambridge University Press:
- 14 May 2010, pp. 541-560
-
- Article
-
- You have access
- Export citation
A Counter-Intuitive Correlation in a Random Tournament
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 13 May 2010, pp. 1-9
-
- Article
- Export citation

Algorithmic Aspects of Graph Connectivity
-
- Published online:
- 07 May 2010
- Print publication:
- 08 September 2008
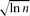 ) and λ ≤ (
) and λ ≤ (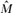
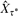 denote the matrix of exit frequencies from singletons to τ* on the reverse chain. We show that
denote the matrix of exit frequencies from singletons to τ* on the reverse chain. We show that 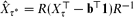 , where
, where 