Refine search
Actions for selected content:
6975 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
Acronyms and Abbreviations
-
- Book:
- Boolean Models and Methods in Mathematics, Computer Science, and Engineering
- Published online:
- 05 June 2013
- Print publication:
- 28 June 2010, pp xvii-xviii
-
- Chapter
- Export citation
12 - Fourier Transforms and Threshold Circuit Complexity
- from Part IV - Graph Representations and Efficient Computation Models
-
-
- Book:
- Boolean Models and Methods in Mathematics, Computer Science, and Engineering
- Published online:
- 05 June 2013
- Print publication:
- 28 June 2010, pp 531-553
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Boolean Models and Methods in Mathematics, Computer Science, and Engineering
- Published online:
- 05 June 2013
- Print publication:
- 28 June 2010, pp i-iv
-
- Chapter
- Export citation
9 - Vectorial Boolean Functions for Cryptography
- from Part III - Learning Theory and Cryptography
-
-
- Book:
- Boolean Models and Methods in Mathematics, Computer Science, and Engineering
- Published online:
- 05 June 2013
- Print publication:
- 28 June 2010, pp 398-470
-
- Chapter
- Export citation

Algorithms on Strings, Trees, and Sequences
- Computer Science and Computational Biology
-
- Published online:
- 23 June 2010
- Print publication:
- 28 May 1997
On the D0L Repetition Threshold
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 3 / July 2010
- Published online by Cambridge University Press:
- 23 June 2010, pp. 281-292
- Print publication:
- July 2010
-
- Article
- Export citation
Parallel Algorithms for Maximal Cliquesin Circle Graphs and Unrestricted Depth Search
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 3 / July 2010
- Published online by Cambridge University Press:
- 23 June 2010, pp. 293-311
- Print publication:
- July 2010
-
- Article
- Export citation
On the Number of Perfect Matchings in Random Lifts
-
- Journal:
- Combinatorics, Probability and Computing / Volume 19 / Issue 5-6 / November 2010
- Published online by Cambridge University Press:
- 09 June 2010, pp. 791-817
-
- Article
- Export citation
Decompositions into Subgraphs of Small Diameter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 19 / Issue 5-6 / November 2010
- Published online by Cambridge University Press:
- 09 June 2010, pp. 753-774
-
- Article
- Export citation
Testing Expansion in Bounded-Degree Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 19 / Issue 5-6 / November 2010
- Published online by Cambridge University Press:
- 09 June 2010, pp. 693-709
-
- Article
- Export citation
The Largest Component in Subcritical Inhomogeneous Random Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 09 June 2010, pp. 131-154
-
- Article
- Export citation
Permuting machines and permutation patterns
-
-
- Book:
- Permutation Patterns
- Published online:
- 05 October 2010
- Print publication:
- 03 June 2010, pp 67-88
-
- Chapter
- Export citation
A survey on partially ordered patterns
-
-
- Book:
- Permutation Patterns
- Published online:
- 05 October 2010
- Print publication:
- 03 June 2010, pp 115-136
-
- Chapter
- Export citation
An introduction to structural methods in permutation patterns
-
-
- Book:
- Permutation Patterns
- Published online:
- 05 October 2010
- Print publication:
- 03 June 2010, pp 153-170
-
- Chapter
- Export citation
Enumeration of partitions by rises, levels and descents
-
-
- Book:
- Permutation Patterns
- Published online:
- 05 October 2010
- Print publication:
- 03 June 2010, pp 221-232
-
- Chapter
- Export citation
Generalized permutation patterns – a short survey
-
-
- Book:
- Permutation Patterns
- Published online:
- 05 October 2010
- Print publication:
- 03 June 2010, pp 137-152
-
- Chapter
- Export citation
Some general results in combinatorial enumeration
-
-
- Book:
- Permutation Patterns
- Published online:
- 05 October 2010
- Print publication:
- 03 June 2010, pp 3-40
-
- Chapter
- Export citation
Packing rates of measures and a conjecture for the packing density of 2413
-
-
- Book:
- Permutation Patterns
- Published online:
- 05 October 2010
- Print publication:
- 03 June 2010, pp 287-316
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Permutation Patterns
- Published online:
- 05 October 2010
- Print publication:
- 03 June 2010, pp i-iv
-
- Chapter
- Export citation
Problems and conjectures
-
-
- Book:
- Permutation Patterns
- Published online:
- 05 October 2010
- Print publication:
- 03 June 2010, pp 339-345
-
- Chapter
- Export citation
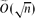 . We prove that the property-testing algorithm proposed by Goldreich and Ron with appropriately set parameters accepts every α-expander with probability at least
. We prove that the property-testing algorithm proposed by Goldreich and Ron with appropriately set parameters accepts every α-expander with probability at least  and rejects every graph that is ϵ-far from any α*-expander with probability at least
and rejects every graph that is ϵ-far from any α*-expander with probability at least 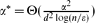 and
and 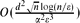 .
.