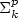Refine search
Actions for selected content:
6975 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
Part VII - Institutions and Aggregate Behavior
-
- Book:
- Networks, Crowds, and Markets
- Published online:
- 05 June 2012
- Print publication:
- 19 July 2010, pp 605-606
-
- Chapter
- Export citation
5 - Positive and Negative Relationships
- from Part I - Graph Theory and Social Networks
-
- Book:
- Networks, Crowds, and Markets
- Published online:
- 05 June 2012
- Print publication:
- 19 July 2010, pp 107-136
-
- Chapter
- Export citation
Part I - Graph Theory and Social Networks
-
- Book:
- Networks, Crowds, and Markets
- Published online:
- 05 June 2012
- Print publication:
- 19 July 2010, pp 19-20
-
- Chapter
- Export citation
Hypergraphs Do Jump
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 13 July 2010, pp. 161-171
-
- Article
- Export citation
On the Influences of Variables on Boolean Functions in Product Spaces
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 09 July 2010, pp. 83-102
-
- Article
- Export citation

Computational Algebraic Geometry
-
- Published online:
- 06 July 2010
- Print publication:
- 29 September 2003

Logical Foundations of Proof Complexity
-
- Published online:
- 06 July 2010
- Print publication:
- 25 January 2010
The 3-Colour Ramsey Number of a 3-Uniform Berge Cycle
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 02 July 2010, pp. 53-71
-
- Article
- Export citation
A Threshold Phenomenon for Random Independent Sets in the Discrete Hypercube
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 02 July 2010, pp. 27-51
-
- Article
- Export citation
Corrigendum to our paper:How Expressions Can Code for Automata
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 3 / July 2010
- Published online by Cambridge University Press:
- 28 July 2010, pp. 339-361
- Print publication:
- July 2010
-
- Article
- Export citation
Balances and Abelian Complexityof a Certain Class of Infinite Ternary Words
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 3 / July 2010
- Published online by Cambridge University Press:
- 20 July 2010, pp. 313-337
- Print publication:
- July 2010
-
- Article
- Export citation
The Uniform Minimum-Ones 2SAT Problemand its Application to Haplotype Classification
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 3 / July 2010
- Published online by Cambridge University Press:
- 28 July 2010, pp. 363-377
- Print publication:
- July 2010
-
- Article
- Export citation
Function operators spanning the arithmetical and the polynomial hierarchy
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 44 / Issue 3 / July 2010
- Published online by Cambridge University Press:
- 05 October 2010, pp. 379-418
- Print publication:
- July 2010
-
- Article
- Export citation
New Graph Polynomials from the Bethe Approximation of the Ising Partition Function
-
- Journal:
- Combinatorics, Probability and Computing / Volume 20 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 30 June 2010, pp. 299-320
-
- Article
- Export citation
Part III - Learning Theory and Cryptography
-
- Book:
- Boolean Models and Methods in Mathematics, Computer Science, and Engineering
- Published online:
- 05 June 2013
- Print publication:
- 28 June 2010, pp 195-196
-
- Chapter
- Export citation
13 - Neural Networks and Boolean Functions
- from Part IV - Graph Representations and Efficient Computation Models
-
-
- Book:
- Boolean Models and Methods in Mathematics, Computer Science, and Engineering
- Published online:
- 05 June 2013
- Print publication:
- 28 June 2010, pp 554-576
-
- Chapter
- Export citation
4 - Probabilistic Analysis of Satisfiability Algorithms
- from Part II - Logic
-
-
- Book:
- Boolean Models and Methods in Mathematics, Computer Science, and Engineering
- Published online:
- 05 June 2013
- Print publication:
- 28 June 2010, pp 99-159
-
- Chapter
- Export citation
Contents
-
- Book:
- Boolean Models and Methods in Mathematics, Computer Science, and Engineering
- Published online:
- 05 June 2013
- Print publication:
- 28 June 2010, pp v-vi
-
- Chapter
- Export citation
Part IV - Graph Representations and Efficient Computation Models
-
- Book:
- Boolean Models and Methods in Mathematics, Computer Science, and Engineering
- Published online:
- 05 June 2013
- Print publication:
- 28 June 2010, pp 471-472
-
- Chapter
- Export citation
8 - Boolean Functions for Cryptography and Error-Correcting Codes
- from Part III - Learning Theory and Cryptography
-
-
- Book:
- Boolean Models and Methods in Mathematics, Computer Science, and Engineering
- Published online:
- 05 June 2013
- Print publication:
- 28 June 2010, pp 257-397
-
- Chapter
- Export citation
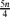 . The result is proved with the Regularity Lemma via the existence of a monochromatic connected matching covering asymptotically 4
. The result is proved with the Regularity Lemma via the existence of a monochromatic connected matching covering asymptotically 4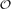
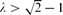 , and nearly matching upper and lower bounds for
, and nearly matching upper and lower bounds for 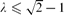 , extending work of Korshunov and Sapozhenko. These bounds allow us to read off some very specific information about the structure of an independent set drawn according to the hard-core distribution.
, extending work of Korshunov and Sapozhenko. These bounds allow us to read off some very specific information about the structure of an independent set drawn according to the hard-core distribution.