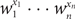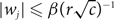Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
Frontmatter
-
- Book:
- Design and Analysis of Algorithms
- Published online:
- 27 April 2019
- Print publication:
- 16 May 2019, pp i-iv
-
- Chapter
- Export citation
8 - String Matching and Finger Printing
-
- Book:
- Design and Analysis of Algorithms
- Published online:
- 27 April 2019
- Print publication:
- 16 May 2019, pp 157-170
-
- Chapter
- Export citation
14 - Parallel Algorithms
-
- Book:
- Design and Analysis of Algorithms
- Published online:
- 27 April 2019
- Print publication:
- 16 May 2019, pp 277-307
-
- Chapter
- Export citation
3 - Warm-up Problems
-
- Book:
- Design and Analysis of Algorithms
- Published online:
- 27 April 2019
- Print publication:
- 16 May 2019, pp 34-53
-
- Chapter
- Export citation
15 - Memory Hierarchy and Caching
-
- Book:
- Design and Analysis of Algorithms
- Published online:
- 27 April 2019
- Print publication:
- 16 May 2019, pp 308-322
-
- Chapter
- Export citation
11 - Maximum Flow and Applications
-
- Book:
- Design and Analysis of Algorithms
- Published online:
- 27 April 2019
- Print publication:
- 16 May 2019, pp 208-229
-
- Chapter
- Export citation
5 - Optimization II: Dynamic Programming
-
- Book:
- Design and Analysis of Algorithms
- Published online:
- 27 April 2019
- Print publication:
- 16 May 2019, pp 92-108
-
- Chapter
- Export citation
9 - Fast Fourier Transform and Applications
-
- Book:
- Design and Analysis of Algorithms
- Published online:
- 27 April 2019
- Print publication:
- 16 May 2019, pp 171-183
-
- Chapter
- Export citation
Appendix A - Recurrences and Generating Functions
-
- Book:
- Design and Analysis of Algorithms
- Published online:
- 27 April 2019
- Print publication:
- 16 May 2019, pp 343-350
-
- Chapter
- Export citation
2 - Basics of Probability and Tail Inequalities
-
- Book:
- Design and Analysis of Algorithms
- Published online:
- 27 April 2019
- Print publication:
- 16 May 2019, pp 16-33
-
- Chapter
- Export citation
16 - Streaming Data Model
-
- Book:
- Design and Analysis of Algorithms
- Published online:
- 27 April 2019
- Print publication:
- 16 May 2019, pp 323-342
-
- Chapter
- Export citation
List of Tables
-
- Book:
- Design and Analysis of Algorithms
- Published online:
- 27 April 2019
- Print publication:
- 16 May 2019, pp xix-xx
-
- Chapter
- Export citation
12 - NP Completeness and Approximation Algorithms
-
- Book:
- Design and Analysis of Algorithms
- Published online:
- 27 April 2019
- Print publication:
- 16 May 2019, pp 230-257
-
- Chapter
- Export citation
A fast new algorithm for weak graph regularity
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 03 May 2019, pp. 777-790
-
- Article
- Export citation

Design and Analysis of Algorithms
- A Contemporary Perspective
-
- Published online:
- 27 April 2019
- Print publication:
- 16 May 2019
Discrete derivative asymptotics of the β-Hermite eigenvalues
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 17 April 2019, pp. 657-674
-
- Article
- Export citation
Weighted counting of solutions to sparse systems of equations
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 15 April 2019, pp. 696-719
-
- Article
- Export citation
Defective and clustered choosability of sparse graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 5 / September 2019
- Published online by Cambridge University Press:
- 12 April 2019, pp. 791-810
-
- Article
- Export citation
Index
-
- Book:
- Proof Complexity
- Published online:
- 25 March 2019
- Print publication:
- 28 March 2019, pp 510-516
-
- Chapter
- Export citation
6 - Algebraic and Geometric Proof Systems
- from Part I - Basic Concepts
-
- Book:
- Proof Complexity
- Published online:
- 25 March 2019
- Print publication:
- 28 March 2019, pp 115-133
-
- Chapter
- Export citation