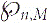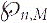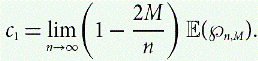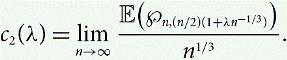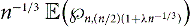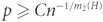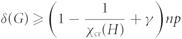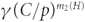Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
3 - Classical Finite-State Automata and Regular Languages
- from Part I - Formal Background
-
- Book:
- Finite-State Techniques
- Published online:
- 29 July 2019
- Print publication:
- 01 August 2019, pp 43-71
-
- Chapter
- Export citation
10 - The Minimal Deterministic Finite-State Automaton for a Finite Language
- from Part II - From Theory to Practice
-
- Book:
- Finite-State Techniques
- Published online:
- 29 July 2019
- Print publication:
- 01 August 2019, pp 253-278
-
- Chapter
- Export citation
Contents
-
- Book:
- Finite-State Techniques
- Published online:
- 29 July 2019
- Print publication:
- 01 August 2019, pp v-viii
-
- Chapter
- Export citation
Preface
-
- Book:
- Finite-State Techniques
- Published online:
- 29 July 2019
- Print publication:
- 01 August 2019, pp ix-x
-
- Chapter
- Export citation
9 - The Aho–Corasick Algorithm
- from Part II - From Theory to Practice
-
- Book:
- Finite-State Techniques
- Published online:
- 29 July 2019
- Print publication:
- 01 August 2019, pp 236-252
-
- Chapter
- Export citation
Index
-
- Book:
- Finite-State Techniques
- Published online:
- 29 July 2019
- Print publication:
- 01 August 2019, pp 302-304
-
- Chapter
- Export citation
11 - Constructing Finite-State Devices for Text Rewriting
- from Part II - From Theory to Practice
-
- Book:
- Finite-State Techniques
- Published online:
- 29 July 2019
- Print publication:
- 01 August 2019, pp 279-297
-
- Chapter
- Export citation
4 - Monoidal Multi-Tape Automata and Finite-State Transducers
- from Part I - Formal Background
-
- Book:
- Finite-State Techniques
- Published online:
- 29 July 2019
- Print publication:
- 01 August 2019, pp 72-93
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Finite-State Techniques
- Published online:
- 29 July 2019
- Print publication:
- 01 August 2019, pp i-iv
-
- Chapter
- Export citation
Part I - Formal Background
-
- Book:
- Finite-State Techniques
- Published online:
- 29 July 2019
- Print publication:
- 01 August 2019, pp 1-2
-
- Chapter
- Export citation
References
-
- Book:
- Finite-State Techniques
- Published online:
- 29 July 2019
- Print publication:
- 01 August 2019, pp 298-301
-
- Chapter
- Export citation
7 - The C(M) language
- from Part II - From Theory to Practice
-
- Book:
- Finite-State Techniques
- Published online:
- 29 July 2019
- Print publication:
- 01 August 2019, pp 161-176
-
- Chapter
- Export citation
6 - Bimachines
- from Part I - Formal Background
-
- Book:
- Finite-State Techniques
- Published online:
- 29 July 2019
- Print publication:
- 01 August 2019, pp 138-158
-
- Chapter
- Export citation
8 - C(M) Implementation of Finite-State Devices
- from Part II - From Theory to Practice
-
- Book:
- Finite-State Techniques
- Published online:
- 29 July 2019
- Print publication:
- 01 August 2019, pp 177-235
-
- Chapter
- Export citation
5 - Deterministic Transducers
- from Part I - Formal Background
-
- Book:
- Finite-State Techniques
- Published online:
- 29 July 2019
- Print publication:
- 01 August 2019, pp 94-137
-
- Chapter
- Export citation

Finite-State Techniques
- Automata, Transducers and Bimachines
-
- Published online:
- 29 July 2019
- Print publication:
- 01 August 2019
Preface
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 25 July 2019, pp. 483-484
-
- Article
-
- You have access
- Export citation
Expected Maximum Block Size in Critical Random Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 25 July 2019, pp. 638-655
-
- Article
- Export citation
On Komlós’ tiling theorem in random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 25 July 2019, pp. 113-127
-
- Article
- Export citation
Erratum to ‘On Percolation and the Bunkbed Conjecture’
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 6 / November 2019
- Published online by Cambridge University Press:
- 22 July 2019, pp. 917-918
-
- Article
-
- You have access
- Export citation