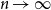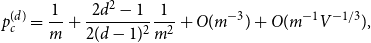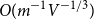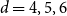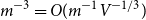Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
References
-
- Book:
- Network Flow Algorithms
- Published online:
- 21 August 2019
- Print publication:
- 05 September 2019, pp 294-306
-
- Chapter
- Export citation
Index
-
- Book:
- Network Flow Algorithms
- Published online:
- 21 August 2019
- Print publication:
- 05 September 2019, pp 310-314
-
- Chapter
- Export citation
9 - Open Questions
-
- Book:
- Network Flow Algorithms
- Published online:
- 21 August 2019
- Print publication:
- 05 September 2019, pp 291-293
-
- Chapter
- Export citation
Preface
-
- Book:
- Network Flow Algorithms
- Published online:
- 21 August 2019
- Print publication:
- 05 September 2019, pp ix-x
-
- Chapter
- Export citation
Author Index
-
- Book:
- Network Flow Algorithms
- Published online:
- 21 August 2019
- Print publication:
- 05 September 2019, pp 307-309
-
- Chapter
- Export citation
7 - Multicommodity Flow Algorithms
-
- Book:
- Network Flow Algorithms
- Published online:
- 21 August 2019
- Print publication:
- 05 September 2019, pp 224-252
-
- Chapter
- Export citation
1 - Preliminaries: Shortest Path Algorithms
-
- Book:
- Network Flow Algorithms
- Published online:
- 21 August 2019
- Print publication:
- 05 September 2019, pp 1-22
-
- Chapter
- Export citation
5 - Minimum-Cost Circulation Algorithms
-
- Book:
- Network Flow Algorithms
- Published online:
- 21 August 2019
- Print publication:
- 05 September 2019, pp 132-187
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Network Flow Algorithms
- Published online:
- 21 August 2019
- Print publication:
- 05 September 2019, pp i-iv
-
- Chapter
- Export citation
8 - Electrical Flow Algorithms
-
- Book:
- Network Flow Algorithms
- Published online:
- 21 August 2019
- Print publication:
- 05 September 2019, pp 253-290
-
- Chapter
- Export citation
4 - More Maximum Flow Algorithms
-
- Book:
- Network Flow Algorithms
- Published online:
- 21 August 2019
- Print publication:
- 05 September 2019, pp 116-131
-
- Chapter
- Export citation
2 - Maximum Flow Algorithms
-
- Book:
- Network Flow Algorithms
- Published online:
- 21 August 2019
- Print publication:
- 05 September 2019, pp 23-79
-
- Chapter
- Export citation
6 - Generalized Flow Algorithms
-
- Book:
- Network Flow Algorithms
- Published online:
- 21 August 2019
- Print publication:
- 05 September 2019, pp 188-223
-
- Chapter
- Export citation
3 - Global Minimum Cut Algorithms
-
- Book:
- Network Flow Algorithms
- Published online:
- 21 August 2019
- Print publication:
- 05 September 2019, pp 80-115
-
- Chapter
- Export citation
Acknowledgements
-
- Book:
- Network Flow Algorithms
- Published online:
- 21 August 2019
- Print publication:
- 05 September 2019, pp xi-xii
-
- Chapter
- Export citation

Network Flow Algorithms
-
- Published online:
- 21 August 2019
- Print publication:
- 05 September 2019
Expansion of Percolation Critical Points for Hamming Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 05 August 2019, pp. 68-100
-
- Article
- Export citation
2 - Monoidal Finite-State Automata
- from Part I - Formal Background
-
- Book:
- Finite-State Techniques
- Published online:
- 29 July 2019
- Print publication:
- 01 August 2019, pp 23-42
-
- Chapter
- Export citation
1 - Formal Preliminaries
- from Part I - Formal Background
-
- Book:
- Finite-State Techniques
- Published online:
- 29 July 2019
- Print publication:
- 01 August 2019, pp 3-22
-
- Chapter
- Export citation
Part II - From Theory to Practice
-
- Book:
- Finite-State Techniques
- Published online:
- 29 July 2019
- Print publication:
- 01 August 2019, pp 159-160
-
- Chapter
- Export citation