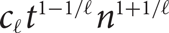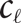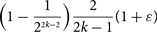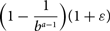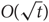Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
Bibliography
-
- Book:
- Communication Complexity
- Published online:
- 30 January 2020
- Print publication:
- 20 February 2020, pp 244-249
-
- Chapter
- Export citation
1 - Deterministic Protocols
- from Part I - Communication
-
- Book:
- Communication Complexity
- Published online:
- 30 January 2020
- Print publication:
- 20 February 2020, pp 9-32
-
- Chapter
- Export citation
Part I - Communication
-
- Book:
- Communication Complexity
- Published online:
- 30 January 2020
- Print publication:
- 20 February 2020, pp 7-8
-
- Chapter
- Export citation
Preface
-
- Book:
- Communication Complexity
- Published online:
- 30 January 2020
- Print publication:
- 20 February 2020, pp xi-xii
-
- Chapter
- Export citation
4 - Numbers on Foreheads
- from Part I - Communication
-
- Book:
- Communication Complexity
- Published online:
- 30 January 2020
- Print publication:
- 20 February 2020, pp 57-66
-
- Chapter
- Export citation
Contents
-
- Book:
- Communication Complexity
- Published online:
- 30 January 2020
- Print publication:
- 20 February 2020, pp vii-x
-
- Chapter
- Export citation
5 - Discrepancy
- from Part I - Communication
-
- Book:
- Communication Complexity
- Published online:
- 30 January 2020
- Print publication:
- 20 February 2020, pp 67-92
-
- Chapter
- Export citation
Percolation on an infinitely generated group
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 20 February 2020, pp. 587-615
-
- Article
- Export citation
9 - Circuits and Proofs
- from Part II - Applications
-
- Book:
- Communication Complexity
- Published online:
- 30 January 2020
- Print publication:
- 20 February 2020, pp 157-174
-
- Chapter
- Export citation
7 - Compressing Communication
- from Part I - Communication
-
- Book:
- Communication Complexity
- Published online:
- 30 January 2020
- Print publication:
- 20 February 2020, pp 121-143
-
- Chapter
- Export citation
8 - Lifting
- from Part I - Communication
-
- Book:
- Communication Complexity
- Published online:
- 30 January 2020
- Print publication:
- 20 February 2020, pp 144-154
-
- Chapter
- Export citation
Index
-
- Book:
- Communication Complexity
- Published online:
- 30 January 2020
- Print publication:
- 20 February 2020, pp 250-252
-
- Chapter
- Export citation
2 - Rank
- from Part I - Communication
-
- Book:
- Communication Complexity
- Published online:
- 30 January 2020
- Print publication:
- 20 February 2020, pp 33-45
-
- Chapter
- Export citation
Analysis of non-reversible Markov chains via similarity orbits
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 18 February 2020, pp. 508-536
-
- Article
- Export citation
Turán numbers of theta graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 13 February 2020, pp. 495-507
-
- Article
- Export citation
On subgraphs of C2k-free graphs and a problem of Kühn and Osthus
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 04 February 2020, pp. 436-454
-
- Article
- Export citation
A note on the Brown–Erdős–Sós conjecture in groups
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 03 February 2020, pp. 633-640
-
- Article
- Export citation

Communication Complexity
- and Applications
-
- Published online:
- 30 January 2020
- Print publication:
- 20 February 2020
Minimax functions on Galton–Watson trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 06 December 2019, pp. 455-484
-
- Article
- Export citation
The replica symmetric phase of random constraint satisfaction problems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 03 December 2019, pp. 346-422
-
- Article
- Export citation