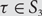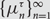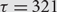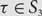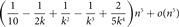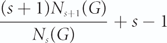Refine search
Actions for selected content:
6974 results in Algorithmics, Complexity, Computer Algebra, Computational Geometry
Avoiding long Berge cycles: the missing cases k = r + 1 and k = r + 2
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 27 November 2019, pp. 423-435
-
- Article
- Export citation
Sharp concentration of the equitable chromatic number of dense random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 26 November 2019, pp. 213-233
-
- Article
- Export citation
Counting higher order tangencies for plane curves
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 26 November 2019, pp. 310-317
-
- Article
- Export citation
Edge-statistics on large graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 14 November 2019, pp. 163-189
-
- Article
- Export citation
Monochromatic trees in random tournaments
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 07 November 2019, pp. 318-345
-
- Article
- Export citation
Surjectivity of near-square random matrices
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 06 November 2019, pp. 267-292
-
- Article
- Export citation
The string of diamonds is nearly tight for rumour spreading
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 04 November 2019, pp. 190-199
-
- Article
- Export citation
Unlabelled Gibbs partitions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 04 November 2019, pp. 293-309
-
- Article
- Export citation
On the Brownian separable permuton
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 24 October 2019, pp. 241-266
-
- Article
- Export citation
On the number of symbols that forces a transversal
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 21 October 2019, pp. 234-240
-
- Article
- Export citation
FKN theorem for the multislice, with applications
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 18 October 2019, pp. 200-212
-
- Article
- Export citation
On Ramsey numbers of hedgehogs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 18 October 2019, pp. 101-112
-
- Article
- Export citation
The Infinite limit of random permutations avoiding patterns of length three
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 14 October 2019, pp. 137-152
-
- Article
- Export citation
On sets of points with few odd secants
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 10 October 2019, pp. 31-43
-
- Article
- Export citation
Minimizing the number of 5-cycles in graphs with given edge-density
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 09 October 2019, pp. 44-67
-
- Article
- Export citation
Extensions of the Erdős–Gallai theorem and Luo’s theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 08 October 2019, pp. 128-136
-
- Article
- Export citation
Long Monotone Trails in Random Edge-Labellings of Random Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 08 October 2019, pp. 22-30
-
- Article
- Export citation
The Induced Removal Lemma in Sparse Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 30 September 2019, pp. 153-162
-
- Article
- Export citation
On the Chromatic Number of Matching Kneser Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 12 September 2019, pp. 1-21
-
- Article
- Export citation
Contents
-
- Book:
- Network Flow Algorithms
- Published online:
- 21 August 2019
- Print publication:
- 05 September 2019, pp v-viii
-
- Chapter
- Export citation