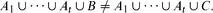Refine search
Actions for selected content:
48287 results in Computer Science
Hypergraphs with No Cycle of a Given Length
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 193-201
-
- Article
- Export citation
18 - Bayesian linear models
- from III - Machine learning
-
- Book:
- Bayesian Reasoning and Machine Learning
- Published online:
- 05 June 2012
- Print publication:
- 02 February 2012, pp 392-411
-
- Chapter
- Export citation
21 - Latent linear models
- from III - Machine learning
-
- Book:
- Bayesian Reasoning and Machine Learning
- Published online:
- 05 June 2012
- Print publication:
- 02 February 2012, pp 462-478
-
- Chapter
- Export citation
A Pair of Forbidden Subgraphs and 2-Factors
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 149-158
-
- Article
- Export citation
9 - Learning as inference
- from II - Learning in probabilistic models
-
- Book:
- Bayesian Reasoning and Machine Learning
- Published online:
- 05 June 2012
- Print publication:
- 02 February 2012, pp 199-242
-
- Chapter
- Export citation
20 - Mixture models
- from III - Machine learning
-
- Book:
- Bayesian Reasoning and Machine Learning
- Published online:
- 05 June 2012
- Print publication:
- 02 February 2012, pp 432-461
-
- Chapter
- Export citation
16 - Supervised linear dimension reduction
- from III - Machine learning
-
- Book:
- Bayesian Reasoning and Machine Learning
- Published online:
- 05 June 2012
- Print publication:
- 02 February 2012, pp 359-366
-
- Chapter
- Export citation
Contents
-
- Book:
- Bayesian Reasoning and Machine Learning
- Published online:
- 05 June 2012
- Print publication:
- 02 February 2012, pp v-xiv
-
- Chapter
- Export citation
Most Probably Intersecting Families of Subsets
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 219-227
-
- Article
- Export citation
Critical Probabilities of 1-Independent Percolation Models
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 11-22
-
- Article
- Export citation
23 - Discrete-state Markov models
- from IV - Dynamical models
-
- Book:
- Bayesian Reasoning and Machine Learning
- Published online:
- 05 June 2012
- Print publication:
- 02 February 2012, pp 489-519
-
- Chapter
- Export citation
The Phase Transition in the Configuration Model
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 265-299
-
- Article
- Export citation
1 - Probabilistic reasoning
- from 1 - Inference in probabilistic models
-
- Book:
- Bayesian Reasoning and Machine Learning
- Published online:
- 05 June 2012
- Print publication:
- 02 February 2012, pp 3-21
-
- Chapter
- Export citation
24 - Continuous-state Markov models
- from IV - Dynamical models
-
- Book:
- Bayesian Reasoning and Machine Learning
- Published online:
- 05 June 2012
- Print publication:
- 02 February 2012, pp 520-546
-
- Chapter
- Export citation
List Colourings of Regular Hypergraphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 315-322
-
- Article
- Export citation
List of notation
-
- Book:
- Bayesian Reasoning and Machine Learning
- Published online:
- 05 June 2012
- Print publication:
- 02 February 2012, pp xx-xx
-
- Chapter
- Export citation
2 - Basic graph concepts
- from 1 - Inference in probabilistic models
-
- Book:
- Bayesian Reasoning and Machine Learning
- Published online:
- 05 June 2012
- Print publication:
- 02 February 2012, pp 22-28
-
- Chapter
- Export citation
2-Cancellative Hypergraphs and Codes
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 159-177
-
- Article
- Export citation
Large Rainbow Matchings in Edge-Coloured Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 255-263
-
- Article
- Export citation
Degree Ramsey Numbers of Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 229-253
-
- Article
- Export citation
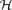
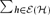
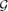
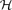
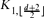 -free graph of minimum degree at least
-free graph of minimum degree at least 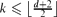 every connected graph
every connected graph 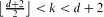 , and prove that only a finite number of connected graphs
, and prove that only a finite number of connected graphs 
 -element subsets. We determine the most probably inclusion-free family too, when the number of members is
-element subsets. We determine the most probably inclusion-free family too, when the number of members is  .
.