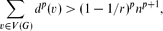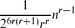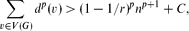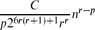Refine search
Actions for selected content:
48287 results in Computer Science
4 - Graphical models
- from 1 - Inference in probabilistic models
-
- Book:
- Bayesian Reasoning and Machine Learning
- Published online:
- 05 June 2012
- Print publication:
- 02 February 2012, pp 58-76
-
- Chapter
- Export citation
Corrádi and Hajnal's Theorem for Sparse Random Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 23-55
-
- Article
- Export citation
Plate Section
-
- Book:
- Bayesian Reasoning and Machine Learning
- Published online:
- 05 June 2012
- Print publication:
- 02 February 2012, pp -
-
- Chapter
- Export citation
22 - Latent ability models
- from III - Machine learning
-
- Book:
- Bayesian Reasoning and Machine Learning
- Published online:
- 05 June 2012
- Print publication:
- 02 February 2012, pp 479-486
-
- Chapter
- Export citation
A coding theoretic study of MLL proof nets
-
- Journal:
- Mathematical Structures in Computer Science / Volume 22 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 409-449
-
- Article
- Export citation
Index
-
- Book:
- Bayesian Reasoning and Machine Learning
- Published online:
- 05 June 2012
- Print publication:
- 02 February 2012, pp 689-697
-
- Chapter
- Export citation
On Even-Degree Subgraphs of Linear Hypergraphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 113-127
-
- Article
- Export citation
10 - Naive Bayes
- from II - Learning in probabilistic models
-
- Book:
- Bayesian Reasoning and Machine Learning
- Published online:
- 05 June 2012
- Print publication:
- 02 February 2012, pp 243-255
-
- Chapter
- Export citation
Star Versus Two Stripes Ramsey Numbers and a Conjecture of Schelp
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 179-186
-
- Article
- Export citation
19 - Gaussian processes
- from III - Machine learning
-
- Book:
- Bayesian Reasoning and Machine Learning
- Published online:
- 05 June 2012
- Print publication:
- 02 February 2012, pp 412-431
-
- Chapter
- Export citation
5 - Efficient inference in trees
- from 1 - Inference in probabilistic models
-
- Book:
- Bayesian Reasoning and Machine Learning
- Published online:
- 05 June 2012
- Print publication:
- 02 February 2012, pp 77-101
-
- Chapter
- Export citation
The Maximum Number of Triangles in C2k+1-Free Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 187-191
-
- Article
- Export citation
V - Approximate inference
-
- Book:
- Bayesian Reasoning and Machine Learning
- Published online:
- 05 June 2012
- Print publication:
- 02 February 2012, pp 585-586
-
- Chapter
- Export citation
BRMLTOOLBOX
-
- Book:
- Bayesian Reasoning and Machine Learning
- Published online:
- 05 June 2012
- Print publication:
- 02 February 2012, pp xxi-xxiv
-
- Chapter
- Export citation
7 - Making decisions
- from 1 - Inference in probabilistic models
-
- Book:
- Bayesian Reasoning and Machine Learning
- Published online:
- 05 June 2012
- Print publication:
- 02 February 2012, pp 127-162
-
- Chapter
- Export citation
IV - Dynamical models
-
- Book:
- Bayesian Reasoning and Machine Learning
- Published online:
- 05 June 2012
- Print publication:
- 02 February 2012, pp 487-488
-
- Chapter
- Export citation
6 - The junction tree algorithm
- from 1 - Inference in probabilistic models
-
- Book:
- Bayesian Reasoning and Machine Learning
- Published online:
- 05 June 2012
- Print publication:
- 02 February 2012, pp 102-126
-
- Chapter
- Export citation
Degree Powers in Graphs: The Erdős–Stone Theorem
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 89-105
-
- Article
- Export citation
My Friend and Colleague, Richard Schelp
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 1-2 / March 2012
- Published online by Cambridge University Press:
- 02 February 2012, pp. 1-9
-
- Article
- Export citation
25 - Switching linear dynamical systems
- from IV - Dynamical models
-
- Book:
- Bayesian Reasoning and Machine Learning
- Published online:
- 05 June 2012
- Print publication:
- 02 February 2012, pp 547-567
-
- Chapter
- Export citation
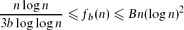
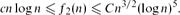
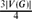 , then in every 2-colouring of the edges of
, then in every 2-colouring of the edges of