Refine search
Actions for selected content:
48290 results in Computer Science
5 - From metrics to networks: The tight span
-
- Book:
- Basic Phylogenetic Combinatorics
- Published online:
- 05 June 2012
- Print publication:
- 15 December 2011, pp 75-103
-
- Chapter
- Export citation
INDEX
-
- Book:
- Proofs and Computations
- Published online:
- 05 January 2012
- Print publication:
- 15 December 2011, pp 457-465
-
- Chapter
- Export citation
Part 3 - Constructive logic and complexity
-
- Book:
- Proofs and Computations
- Published online:
- 05 January 2012
- Print publication:
- 15 December 2011, pp 247-248
-
- Chapter
- Export citation
9 - Rooted trees and the Farris transform
-
- Book:
- Basic Phylogenetic Combinatorics
- Published online:
- 05 June 2012
- Print publication:
- 15 December 2011, pp 195-221
-
- Chapter
- Export citation
CHAPTER 1 - LOGIC
- from Part 1 - Basic proof theory and computability
-
- Book:
- Proofs and Computations
- Published online:
- 05 January 2012
- Print publication:
- 15 December 2011, pp 5-60
-
- Chapter
- Export citation
CHAPTER 2 - RECURSION THEORY
- from Part 1 - Basic proof theory and computability
-
- Book:
- Proofs and Computations
- Published online:
- 05 January 2012
- Print publication:
- 15 December 2011, pp 61-112
-
- Chapter
- Export citation
CHAPTER 8 - LINEAR TWO-SORTED ARITHMETIC
- from Part 3 - Constructive logic and complexity
-
- Book:
- Proofs and Computations
- Published online:
- 05 January 2012
- Print publication:
- 15 December 2011, pp 395-430
-
- Chapter
- Export citation
CHAPTER 6 - COMPUTABILITY IN HIGHER TYPES
- from Part 3 - Constructive logic and complexity
-
- Book:
- Proofs and Computations
- Published online:
- 05 January 2012
- Print publication:
- 15 December 2011, pp 249-312
-
- Chapter
- Export citation
CHAPTER 4 - THE PROVABLY RECURSIVE FUNCTIONS OF ARITHMETIC
- from Part 2 - Provable recursion in classical systems
-
- Book:
- Proofs and Computations
- Published online:
- 05 January 2012
- Print publication:
- 15 December 2011, pp 149-194
-
- Chapter
- Export citation
Index
-
- Book:
- Basic Phylogenetic Combinatorics
- Published online:
- 05 June 2012
- Print publication:
- 15 December 2011, pp 261-264
-
- Chapter
- Export citation
2 - Encoding X-trees
-
- Book:
- Basic Phylogenetic Combinatorics
- Published online:
- 05 June 2012
- Print publication:
- 15 December 2011, pp 21-30
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Proofs and Computations
- Published online:
- 05 January 2012
- Print publication:
- 15 December 2011, pp i-vi
-
- Chapter
- Export citation
PRELIMINARIES
-
- Book:
- Proofs and Computations
- Published online:
- 05 January 2012
- Print publication:
- 15 December 2011, pp 1-2
-
- Chapter
- Export citation
3 - Consistency of X-tree encodings
-
- Book:
- Basic Phylogenetic Combinatorics
- Published online:
- 05 June 2012
- Print publication:
- 15 December 2011, pp 31-49
-
- Chapter
- Export citation
Preface
-
- Book:
- Basic Phylogenetic Combinatorics
- Published online:
- 05 June 2012
- Print publication:
- 15 December 2011, pp ix-xii
-
- Chapter
- Export citation
Commonly used symbols
-
- Book:
- Basic Phylogenetic Combinatorics
- Published online:
- 05 June 2012
- Print publication:
- 15 December 2011, pp 242-252
-
- Chapter
- Export citation
CHAPTER 3 - GÖDEL'S THEOREMS
- from Part 1 - Basic proof theory and computability
-
- Book:
- Proofs and Computations
- Published online:
- 05 January 2012
- Print publication:
- 15 December 2011, pp 113-146
-
- Chapter
- Export citation
BIBLIOGRAPHY
-
- Book:
- Proofs and Computations
- Published online:
- 05 January 2012
- Print publication:
- 15 December 2011, pp 431-456
-
- Chapter
- Export citation
Formalising PFSQL queries using ŁΠ
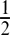 fuzzy logic†
fuzzy logic†
-
- Journal:
- Mathematical Structures in Computer Science / Volume 22 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 14 December 2011, pp. 533-547
-
- Article
- Export citation
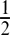 fuzzy logic
fuzzy logic
