Refine search
Actions for selected content:
48581 results in Computer Science
Notes on the theory of scales
- from PART I - GAMES AND SCALES
-
-
- Book:
- Games, Scales and Suslin Cardinals
- Published online:
- 06 January 2010
- Print publication:
- 15 September 2008, pp 28-74
-
- Chapter
- Export citation
Scales in K(ℝ)
- from PART I - GAMES AND SCALES
-
-
- Book:
- Games, Scales and Suslin Cardinals
- Published online:
- 06 January 2010
- Print publication:
- 15 September 2008, pp 176-208
-
- Chapter
- Export citation
Scales on coinductive sets
- from PART I - GAMES AND SCALES
-
-
- Book:
- Games, Scales and Suslin Cardinals
- Published online:
- 06 January 2010
- Print publication:
- 15 September 2008, pp 102-109
-
- Chapter
- Export citation
On the Connectivity of Random k-th Nearest Neighbour Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 343-362
-
- Article
- Export citation
Threshold Functions for Markov Chains: a Graph Theoretic Approach
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. 351-362
-
- Article
- Export citation
Constructing Small Sets that are Uniform in Arithmetic Progressions
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. 513-518
-
- Article
- Export citation
CPC volume 5 issue 3 Cover and Front matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Computing Norms of Group-Invariant Transition Operators
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. 161-178
-
- Article
- Export citation
Restricted Edge-colourings of Bipartite Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 4 / December 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. 385-392
-
- Article
- Export citation
CPC volume 5 issue 1 Cover and Front matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Aaron Halpern On the Placement and Morphology of Clitics, Stanford, CA, 1995. ISBN 1 881 52660 7, £17.95 (paperback). ISBN 1 881 52661 5, £35.00 (hardback).
-
- Journal:
- Natural Language Engineering / Volume 1 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 393-396
-
- Article
- Export citation
CPC volume 5 issue 1 Cover and Back matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. b1-b4
-
- Article
-
- You have access
- Export citation
CPC volume 1 issue 1 Cover and Back matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. b1-b3
-
- Article
-
- You have access
- Export citation
Upper Bounds for the Connective Constant of Self-Avoiding Walks
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. 115-136
-
- Article
- Export citation
Topological Cliques in Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. 247-256
-
- Article
- Export citation
The Smallest Cubic Graphs of Girth Nine
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 317-329
-
- Article
- Export citation
Menger's Theorem for a Countable Source Set
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. 145-156
-
- Article
- Export citation
A Ramsey-Type Theorem in the Plane
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. 127-135
-
- Article
- Export citation
A Theorem on Reconstruction of Random Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. 1-9
-
- Article
- Export citation
On Intersecting Chains in Boolean Algebras
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. 57-62
-
- Article
- Export citation
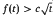 . Here we prove the weaker estimate
. Here we prove the weaker estimate 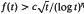 .
.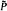 ,
, 