Refine search
Actions for selected content:
48580 results in Computer Science
Additive and Multiplicative Ramsey Theorems in ℕ – Some Elementary Results†
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. 221-241
-
- Article
- Export citation
CPC volume 4 issue 1 Cover and Back matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Duality in Polymatroids and Set Functions
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. 275-280
-
- Article
- Export citation
CPC volume 2 issue 2 Cover and Back matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation
High speed feature unification and parsing
-
- Journal:
- Natural Language Engineering / Volume 1 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 309-338
-
- Article
- Export citation
A Randomised Approximation Algorithm for Counting the Number of Forests in Dense Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. 273-283
-
- Article
- Export citation
CPC volume 2 issue 4 Cover and Front matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
On Extremal Set Partitions in Cartesian Product Spaces
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. 211-220
-
- Article
- Export citation
Finding a Longest Alternating Cycle in a 2-edge-coloured Complete Graph is in RP
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. 297-306
-
- Article
- Export citation
E. Ashcroft, A. Faustini, Anthony, R. Jagannathan and W. Wadge, Multi-dimensional programming. New York, NY: Oxford University Press, 1995. ISBN 019 507597 8, £40.00.
-
- Journal:
- Natural Language Engineering / Volume 1 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 390-392
-
- Article
- Export citation
Anaphora and ellipsis in artificial languages
-
- Journal:
- Natural Language Engineering / Volume 1 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 217-234
-
- Article
- Export citation
A rule-based phrase parser for real-time text-to-speech synthesis
-
- Journal:
- Natural Language Engineering / Volume 1 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 191-212
-
- Article
- Export citation
Automorphisms of Dowling Lattices and Related Geometries
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 1-9
-
- Article
- Export citation
Editorial: In Honour of Paul Erdős
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 12 September 2008, p. 101
-
- Article
-
- You have access
- Export citation
Editorial
-
- Journal:
- Natural Language Engineering / Volume 1 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 1-8
-
- Article
-
- You have access
- Export citation
The Harmonious Chromatic Number of Almost All Trees
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 31-46
-
- Article
- Export citation
The Strongly Connected Components of 1-in, 1-out
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. 265-274
-
- Article
- Export citation
Amalgamated Factorizations of Complete Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. 215-232
-
- Article
- Export citation
Random Permutations: Some Group-Theoretic Aspects
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. 257-262
-
- Article
- Export citation
On Recognition of Shift Registers
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. 307-315
-
- Article
- Export citation
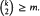 ≥
≥ 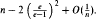 .
.