Refine search
Actions for selected content:
48579 results in Computer Science
Best parse parsing with Earley's and Inside algorithms on probabilistic RTN
-
- Journal:
- Natural Language Engineering / Volume 1 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 147-161
-
- Article
- Export citation
How Do Read-Once Formulae Shrink?
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. 455-469
-
- Article
- Export citation
t-Covering Arrays: Upper Bounds and Poisson Approximations
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. 105-117
-
- Article
- Export citation
Editorial: Issues Dedicated to Paul Erdős
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 12 September 2008, p. i
-
- Article
-
- You have access
- Export citation
A Combinatorial Approach to Complexity Theory via Ordinal Hierarchies
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. 177-190
-
- Article
- Export citation
On a Correlation Inequality of Farr
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. 157-160
-
- Article
- Export citation
Nearly Equal Distances in the Plane
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. 401-408
-
- Article
- Export citation
A Characterization of Almost-Planar Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. 227-245
-
- Article
- Export citation
Sign-Coherent Identities for Characteristic Polynomials of Matroids
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. 33-51
-
- Article
- Export citation
Substitution Method Critical Probability Bounds for the Square Lattice Site Percolation Model
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 181-188
-
- Article
- Export citation
Large Induced Subgraphs with All Degrees Odd
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. 335-349
-
- Article
- Export citation
An Upper Bound on Zarankiewicz' Problem
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. 29-33
-
- Article
- Export citation
Lattice Points of Cut Cones
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. 191-214
-
- Article
- Export citation
Recognizing Polymatroids Associated with Hypergraphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. 519-530
-
- Article
- Export citation
Using the Perceptron Algorithm to Find Consistent Hypotheses
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. 385-387
-
- Article
- Export citation
Optimal Strategy for the First Player in the Penney Ante Game
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. 311-321
-
- Article
- Export citation
A Group-Theoretic Setting for Some Intersecting Sperner Families
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. 323-334
-
- Article
- Export citation
A Mildly Exponential Time Algorithm for Approximating the Number of Solutions to a Multidimensional Knapsack Problem
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. 271-284
-
- Article
- Export citation
CPC volume 2 issue 3 Cover and Back matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation
An Expanded Set of Correlation Tests for Linear Congruential Random Number Generators*
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. 161-168
-
- Article
- Export citation
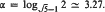 . This result is asymptotically the tightest possible. It improves a similar result obtained recently by Håstad, Razborov and Yao.
. This result is asymptotically the tightest possible. It improves a similar result obtained recently by Håstad, Razborov and Yao.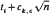 for some 1 ≤
for some 1 ≤ 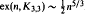 .
.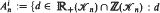 has exactly
has exactly 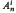 is infinite, except for the undecided case
is infinite, except for the undecided case 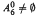 and empty
and empty 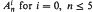 and for
and for 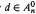 ; we also estimate such scales for classes of points. We construct families of points of
; we also estimate such scales for classes of points. We construct families of points of 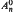 and ℤ
and ℤ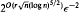 time randomized algorithm that estimates the number of feasible solutions of a multidimensional knapsack problem within 1 ±
time randomized algorithm that estimates the number of feasible solutions of a multidimensional knapsack problem within 1 ± 