This is a survey of a number of recent papers dealing with graphs from a geometric perspective. The main theme of these studies is the relationship between graph properties that are local in nature, and global graph parameters. Connections with the theory of distributed computing are pointed out and many open problems are presented.

We consider the performance of a simple greedy matching algorithm MINGREEDY when applied to random cubic graphs. We show that if λn is the expected number of vertices not matched by MINGREEDY, there are positive constants c1 and c2 such that C1n1/5 ≤ λn ≤ C2n1/5 log n.

We define and efficiently compute the canonical flow on a graph, which is a certain feasible solution for the concurrent flow problem and exhibits invariance under the action of the automorphism group of the graph. Using estimates for the congestion of our canonical flow, we derive lower bounds on the crossing number, bisection width, and the edge and vertex expansion of a graph in terms of sizes of the edge and vertex orbits and the average distance in the graph. We further exhibit classes of graphs for which our lower bounds are tight within a multiplicative constant. Also, in cartesian product graphs a concurrent flow is constructed in terms of the concurrent flows in the factors, and in this way lower bounds for the edge and vertex expansion of the power graphs are derived in terms of that of the original graph.

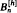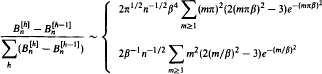
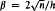The number, , of rooted plane binary trees of height ≤ h with n internal nodes is shown to satisfy

uniformly for δ−1(log n)−1/2 ≤ β ≤ δ(log n)1/2, where and δ is a positive constant. An asymptotic formula for 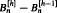is derived for 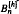h = cn, where 0 < c < 1. Bounds for are also derived for large and small heights. The methods apply to any simple family of trees, and the general asymptotic results are stated.

One of our results: let X be a finite set on the plane, 0 < ε < 1, then there exists a set F (a weak ε-net) of size at most 7/ε2 such that every convex set containing at least ε|X| elements of X intersects F. Note that the size of F is independent of the size of X.

Motivated by the problem of making correct computations from partly false information, we study a corruption of the classic game “Twenty Questions” in which the player who answers the yes-or-no questions is permitted to lie up to a fixed fraction r of the time. The other player is allowed q arbitrary questions with which to try to determine, with certainty, which of n objects his opponent has in mind; he “wins” if he can always do so, and “wins quickly” if he can do so using only O(log n) questions.

It turns out that there is a threshold value for r below which the querier can win quickly, and above which he cannot win at all. However, the threshold value varies according to the precise rules of the game. Our “three thresholds theorem” says that when the answerer is forbidden at any point to have answered more than a fraction r of the questions incorrectly, then the threshold value is r = ½; when the requirement is merely that the total number of lies cannot exceed rq, the threshold is ⅓; and finally if the answerer gets to see all the questions before answering, the threshold drops to ¼.

Robertson and Seymour proved that excluding any fixed forest F as a minorimposes a bound on the path-width of a graph. We give a short proof of this, reobtaining the best possible bound of |F| – 2.

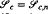Let S be a set of m clauses each containing three literals chosen at random in a set {p1, ¬p1,…,pn, ¬pn} of n propositional variables and their negations. Let be the set of all such 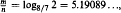S with m = cn for a fixed c > 0. We show, improving significantly over the first moment upper bound , that if 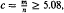m and n tend to infinity with , then almost all 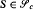are unsatisfiable.

In this paper, asymptotical estimates of the form Rn(1+o(1)) for various classes of planar valency-restricted Eulerian maps are established. It follows, in particular, that ‘almost all’ (as n → ∞) n-edged planar Eulerian maps have n/3 (1+o(1)) vertices. A brief survey of known asymptotical results (a table of values of R) for various classes of planar maps is also presented.

In this paper we consider the following problem, given a graph H, what is the structure of a typical, i.e. random, H-free graph? We completely solve this problem for all graphs H containing a critical vertex. While this result subsumes a sequence of known results, its short proof is self contained.

A Steiner quadruple system SQS(v) of order v is a family ℬ of 4-element subsets of a v-element set V such that each 3-element subset of V is contained in precisely one B ∈ ℬ. We prove that if T ∩ B ≠ ø for all B ∈ ℬ (i.e., if T is a transversal), then |T| ≥ v/2, and if T is a transversal of cardinality exactly v/2, then V \ T is a transversal as well (i.e., T is a blocking set). Also, in respect of the so-called ‘doubling construction’ that produces SQS(2v) from two copies of SQS(v), we give a necessary and sufficient condition for this operation to yield a Steiner quadruple system with blocking sets.

We consider the set of polynomials of degree n over a finite field and put the uniform probability measure on this set. Any such polynomial factors uniquely into a product of its irreducible factors. To each polynomial we associate a step function on the interval [0,1] such that the size of each jump corresponds to the number of factors of a certain degree in the factorization of the random polynomial. We normalize these random functions and show that the resulting random process converges weakly to Brownian motion as n → ∞. This result complements earlier work by the author on the order statistics of the degree sequence of the factors of a random polynomial.

A graph G is called n-minimizable if it can be reduced, by deleting a set of its edges, to a minimally n-connected graph. It is shown that, if n-connected graphs G and H differ only by finitely many vertices and edges, then G is n-minimizable if and only if H is n-minimizable (Theorem 4.12). In the main result, conditions are given that a tree decomposition of an n-connected graph G must satisfy in order to guarantee that the n-minimizability of each of the members of this decomposition implies the n-minimizability of the graph G (Theorem 6.5).

This paper gives precise isoperimetric inequalities for infinite graphs on which a group acts with finite quotient. Decay estimates are obtained for the iterated kernels of the associated random walks.