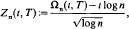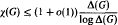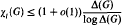Refine search
Actions for selected content:
48584 results in Computer Science
Conditional Independences among Four Random Variables II
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 407-417
-
- Article
- Export citation
Properties of Classes of Random Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. 435-454
-
- Article
- Export citation
The Computational Complexity of the Tutte Plane: the Bipartite Case
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. 181-187
-
- Article
- Export citation
Predecessors in Random Mappings
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 4 / December 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. 317-335
-
- Article
- Export citation
Random Matrices and Brownian Motion†
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. 157-180
-
- Article
- Export citation
Randomised Approximation in the Tutte Plane
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. 137-143
-
- Article
- Export citation
CPC volume 4 issue 3 Cover and Front matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
A Rate for the Erdős-Turán Law*
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. 167-176
-
- Article
- Export citation
On Random Generation of the Symmetric Group
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. 505-512
-
- Article
- Export citation
Some Small Circuit-Cocircuit Ramsey Numbers for Matroids
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 67-80
-
- Article
- Export citation
Choice Numbers of Graphs: a Probabilistic Approach
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. 107-114
-
- Article
- Export citation
Hamilton Cycles in Random Regular Digraphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. 39-49
-
- Article
- Export citation
CPC volume 3 issue 4 Cover and Front matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Matchings in Lattice Graphs and Hamming Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. 157-166
-
- Article
- Export citation
On the Hardness of Approximating Some Optimization Problems That Are Supposedly Easier Than MAX CLIQUE
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 167-180
-
- Article
- Export citation
A Winning Strategy for the Ramsey Graph Game
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. 267-276
-
- Article
- Export citation
A Phase Transition for the Distribution of Matching Blocks
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. 139-159
-
- Article
- Export citation
Several knowledge models and a blackboard memory for human-machine robust dialogues
-
- Journal:
- Natural Language Engineering / Volume 1 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 113-145
-
- Article
- Export citation
On the Structure of Non-Hamiltonian Graphs I
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. 27-34
-
- Article
- Export citation
On Brooks' Theorem for Sparse Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 97-132
-
- Article
- Export citation
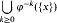 are called the predecessors of
are called the predecessors of