Refine search
Actions for selected content:
48572 results in Computer Science
Author Index to Volume 4
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 443-444
-
- Article
- Export citation
CPC volume 3 issue 4 Cover and Back matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 12 September 2008, p. b1
-
- Article
-
- You have access
- Export citation
Valid Generalisation from Approximate Interpolation
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. 191-214
-
- Article
- Export citation
On the Diameter of Random Cayley Graphs of the Symmetric Group
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. 201-208
-
- Article
- Export citation
On the Number of Hamiltonian Cycles in Bipartite Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 4 / December 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. 437-442
-
- Article
- Export citation
Perfect Hashing and Probability
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. 407-409
-
- Article
- Export citation
CPC volume 3 issue 1 Cover and Back matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 12 September 2008, p. b1
-
- Article
-
- You have access
- Export citation
CPC volume 2 issue 4 Cover and Back matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Proof of a Packing Conjecture of Bollobás
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 241-255
-
- Article
- Export citation
Topological cliques in graphs II
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. 79-90
-
- Article
- Export citation
First Occurrence in Pairs of Long Words: A Penney-ante Conjecture of Pevzner
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 279-285
-
- Article
- Export citation
Almost Every Graph can be Covered by
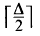 Linear Forests
Linear Forests
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 257-268
-
- Article
- Export citation
CPC volume 3 issue 3 Cover and Back matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 12 September 2008, p. b1
-
- Article
-
- You have access
- Export citation
Complete Subgraphs of r-partite Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. 241-250
-
- Article
- Export citation
Smallest Sets of Longest Paths with Empty Intersection
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 4 / December 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. 429-436
-
- Article
- Export citation
Russian morphology: An engineering approach
-
- Journal:
- Natural Language Engineering / Volume 1 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 235-260
-
- Article
- Export citation
Improved Upper Bounds Concerning the Erdős-Ko-Rado Theorem
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. 115-122
-
- Article
- Export citation
On Vertices of Degree n in Minimally n-Edge-Connected Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 81-95
-
- Article
- Export citation
Random Regular Graphs: Asymptotic Distributions and Contiguity
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 369-405
-
- Article
- Export citation
Non-Binary Matroids Having At Most Three Non-Binary Elements
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. 355-369
-
- Article
- Export citation
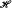 and
and 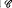 be sets of functions from domain
be sets of functions from domain  on
on 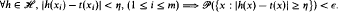
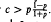 . For |
. For |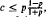 , then the conjecture is true when
, then the conjecture is true when 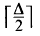 Linear Forests
Linear Forests
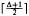 linear forests. We show that almost every graph can be covered with this number of linear forests.
linear forests. We show that almost every graph can be covered with this number of linear forests.