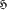Let be the hypergraph whose points are the subsets 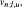X of [n] := {1,…,n} with l≤ |X| ≤ u, l < u, and whose edges are intervals in the Boolean lattice of the form I = {C ⊆[n] : X⊆C⊆Y} where |X| = l, |Y| = u, X ⊆ Y.We study the matching number i.e. the the maximum number of pairwise disjoint edges, and the covering number 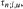i.e. the minimum number of points which cover all edges. We prove that max 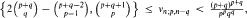and that for every ε > 0 the inequalities 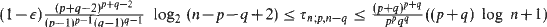hold, where for the lower bounds we suppose that n is not too small. The corresponding fractional numbers can be determined exactly. Moreover, we show by construction that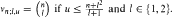

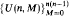A dominating set for a graph G is a set D of vertices of G such that every vertex of G not in D is adjacent to a vertex of D. We prove that any graph G of minimum degree at least three contains a dominating set D of size at most 3|V(G)|/8. A star S is a graph consisting of a centre x and a set of edges from x to S — x. Clearly, a dominating set D for a graph G corresponds to a set of |D| stars which cover V(G). Thus, we show that the vertices of any graph G of minimum degree 3 can be covered by at most 3|V(G)|/8 vertex disjoint stars. We also show that any connected cubic graph G can be covered by [|V(G)|/9] vertex disjoint paths. Both these results are sharp.

There is a close relationship between biased graph games and random graph processes. In this paper, we develop the analogy and give further interesting instances.

It is shown that an oriented graph of order n whose every indegree and outdegree is at least cn is hamiltonian if c ≥ ½ − 2−15 but need not be if c < ⅜.

A definition is adopted for convexity of a set of directed lines in the plane. Following this, the duals of a number of standard problems of geometric probability are formulated. Problems considered in detail are the duals of Sylvester's problem, chord length distributions and Ambartzumian's combinatorial geometry. The paper suggests some questions for further work.

We describe a very simple method of randomly permuting the cube {0, 1}n such that the sample space is very small, but, given any m distinct points in {0, 1}n, the images of those points under the random permutation are approximately uniformly distributed over all sequences of m distinct points.

Let S be a closed surface with boundary ∂S and let G be a graph. Let K ⊆ G be a subgraph embedded in S such that ∂S ⊆ K. An embedding extension of K to G is an embedding of G in S that coincides on K with the given embedding of K. Minimal obstructions for the existence of embedding extensions are classified in cases when S is the disk or the cylinder. Linear time algorithms are presented that either find an embedding extension, or return an obstruction to the existence of extensions. These results are to be used as the corner stones in the design of linear time algorithms for the embeddability of graphs in an arbitrary surface and for solving more general embedding extension problems.

We show that the random insertion method for the traveling salesman problem (TSP) may produce a tour Ω(log log n/log log log n) times longer than the optimal tour. The lower bound holds even in the Euclidean Plane. This is in contrast to the fact that the random insertion method performs extremely well in practice. In passing, we show that other insertion methods may produce tours Ω(log n/log log n) times longer than the optimal one. No non-constant lower bounds were previously known.

We study the asymptotic properties of a “uniform” random graph process in which the minimum degree of U(n, M) grows at least as fast as ⌊M/n⌋. We show that if M — n → → ∞, almost surely U(n, M) consists of one giant component and some number of small unicyclic components. We go on to study the distribution of cycles in unicyclic components as they emerge at the beginning of the process and disappear when captured by the giant one.

Let k be a positive integer, k ≥ 2. In this paper we study bipartite graphs G such that, for n sufficiently large, each two-coloring of the edges of the complete graph Kn gives a monochromatic copy of G, with some k of its vertices having the maximum degree of these k vertices minus the minimum degree of these k vertices (in the colored Kn) at most k − 2.

A connection is made between the theory of ergodicity and the expected complexity of string searching. In particular, a substring search algorithm is introduced which, when applied to searching in text that has been produced by an appropriate stationary ergodic source, has an expected running time of O((N/m + m)logm), for a text string of length N and search string of length m. Similar expected complexity results have been obtained before, but the analysis is performed in a significantly more general framework, which models with greater accuracy the statistics of many types of strings, including natural language. The analysis also sheds light on the performance of the Boyer-Moore algorithm and the Sunday algorithm when applied to natural language.

A theorem of Makarov states that the harmonic measure of a connected subset of ℝ2 is supported on a set of Hausdorff dimension one. This paper gives an analogue of this theorem for discrete harmonic measure, i.e., the hitting measure of simple random walk. It is proved that for any 1/2 < α < 1, β < α − 1/2, there is a constant k such that for any connected subset A ⊂ ℤ2 of radius n,

where HA denotes discrete harmonic measure.