We derive bounds for eigenvalues of the Laplacian of graphs using discrete versions of the Sobolev inequalities and heat kernel estimates.

We show that the total chromatic number of a simple k-chromatic graph exceeds the chromatic index by at most 18k ⅓ log ½ 3k.

For every n consider a subset Hn of the patterns of length n over a fixed finite alphabet. The limit distribution of the waiting time until each element of Hn appears in an infinite sequence of independent, uniformly distributed random letters was determined in an earlier paper. This time we prove that these waiting times are getting independent as n → ∞. Our result is used for applying the converse part of the Borel–Cantelli lemma to problems connected with such waiting times, yielding thus improvements on some known theorems.

Shannon (1948) showed that a wide range of practical problems can be reduced to the problem of estimating probability distributions of words and ngrams in text. It has become standard practice in text compression, speech recognition, information retrieval and many other applications of Shannon's theory to introduce a “bag-of-words” assumption. But obviously, word rates vary from genre to genre, author to author, topic to topic, document to document, section to section, and paragraph to paragraph. The proposed Poisson mixture captures much of this heterogeneous structure by allowing the Poisson parameter θ to vary over documents subject to a density function φ. φ is intended to capture dependencies on hidden variables such genre, author, topic, etc. (The Negative Binomial is a well-known special case where φ is a Г distribution.) Poisson mixtures fit the data better than standard Poissons, producing more accurate estimates of the variance over documents (σ2), entropy (H), inverse document frequency (IDF), and adaptation (Pr(x ≥ 2/x ≥ 1)).

We consider a simple randomised algorithm that seeks a weak 2-colouring of a hypergraph H; that is, it tries to 2-colour the points of H so that no edge is monochromatic. If H has a particular well-behaved form of such a colouring, then the method is successful within expected number of iterations O(n3) when H has n points. In particular, when applied to a graph G with n nodes and chromatic number 3, the method yields a 2-colouring of the vertices such that no triangle is monochromatic in expected time O(n4).

An infinite graph is called bounded if for every labelling of its vertices with natural numbers there exists a sequence of natural numbers which eventually exceeds the labelling along any ray in the graph. Thomassen has conjectured that a countable graph is bounded if and only if its edges can be oriented, possibly both ways, so that every vertex has finite out-degree and every ray has a forward oriented tail. We present a counterexample to this conjecture.

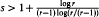We show that r-regular, s-uniform hypergraphs contain a perfect matching with high probability (whp), provided The Proof is based on the application of a technique of Robinson and Wormald [7, 8]. The space of hypergraphs is partitioned into subsets according to the number of small cycles in the hypergraph. The difference in the expected number of perfect matchings between these subsets explains most of the variance of the number of perfect matchings in the space of hypergraphs, and is sufficient to prove existence (whp), using the Chebychev Inequality.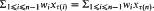

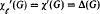The main result of this paper is that for every 2 ≤ r < s, and n sufficiently large, there exist graphs of order n, not containing a complete graph on s vertices, in which every relatively not too small subset of vertices spans a complete graph on r vertices. Our results improve on previous results of Bollobás and Hind.

It is proved that any plane graph may be represented by a triangle contact system, that is a collection of triangular disks which are disjoint except at contact points, each contact point being a node of exactly one triangle. Representations using contacts of T-or Y-shaped objects follow. Moreover, there is a one-to-one mapping between all the triangular contact representations of a maximal plane graph and all its partitions into three Schnyder trees.

A graph is vertex-transitive (edge-transitive) if its automorphism group acts transitively on the vertices (edges, resp.). The expansion rate of a subset S of the vertex set is the quotient e(S):= |∂(S)|/|S|, where ∂(S) denotes the set of vertices not in S but adjacent to some vertex in S. Improving and extending previous results of Aldous and Babai, we give very simple proofs of the following results. Let X be a (finite or infinite) vertex-transitive graph and let S be a finite subset of the vertices. If X is finite, we also assume |S| ≤|V(X)/2. Let d be the diameter of S in the metric induced by X. Then e(S) ≥1/(d + 1); and e(S) ≥ 2/(d +2) if X is finite and d is less than the diameter of X. If X is edge-transitive then |δ(S)|/|S| ≥ r/(2d), where ∂(S) denotes the set of edges joining S to its complement and r is the harmonic mean of the minimum and maximum degrees of X. – Diverse applications of the results are mentioned.

The main result of this paper has the following consequence. Let G be an abelian group of order n. Let {xi: 1 ≤ 2n − 1} be a family of elements of G and let {wi: 1 ≤ i ≤ n − 1} be a family of integers prime relative to n. Then there is a permutation & of [1,2n − 1] such that

Applying this result with wi = 1 for all i, one obtains the Erdős–Ginzburg–Ziv Theorem.

Thinking of a deterministic function s: ℤ → ℕ as ‘scenery’ on the integers, a simple random walk on ℤ generates a random record of scenery ‘observed’ along the walk. We address this question: If t:ℤ → ℕ is another scenery on the integers and we are handed a random scenery record obtained from either s or t, under what circumstances can the source be distinguished? We allow ourselves to use information about s and t together with information contained in the scenery record. It has been conjectured that it is sufficient for t to be neither a translate of s nor a translate of the reflection of s. We show that this condition is sufficient to ensure distinguishability if s−1(δ) is finite and non-empty for some δ ∈ℕ.

Let G be a graph and P(G, t) be the chromatic polynomial of G. It is known that P(G, t) has no zeros in the intervals (−∞, 0) and (0, 1). We shall show that P(G, t) has no zeros in (1, 32/27]. In addition, we shall construct graphs whose chromatic polynomials have zeros arbitrarily close to 32/27.

In this paper, we present a techique for examining all trees of a given order. Our approach is based on the Beyer and Hedetniemi algorithm for generating all rooted trees of a given order and on the Wright, Richmond, Odlyzko and McKay algorithm for generating all free trees of a given order. In the introduction we describe these algorithms. We also give a precise evaluation of the average number of moves it takes to generate a rooted tree, which improves the upper bound given by Beyer and Hedetniemi. In the second section we present a new method of examining all trees which uses these generating algorithms. The last section contains two applications of the method introduced. The main result of the paper is that the average number of steps required by the proposed algorithm to examine a rooted tree is bounded by a constant independent of the order of a tree.

Recently, Galvin [7] proved that every k-edge-colourable bipartite multigraph is k-edge-choosable. In particular, for a bipartite multigraph G, . Here we give a brief self-contained proof of this result.

A transformation that increases the blocking probability of the channel graphs arising in interconnection networks is developed. This provides the basis for eminently computing a bound on the blocking probability by applying the transformation to reduce an arbitrary four-stage channel graph to a threshold channel graph. The four-stage channel graph that is most likely to block, given links that are equally likely to block, is characterized. Partial results are proved concerning the threshold channel graphs that are least likely to block.

We consider the problem of broadcasting in an n–node hypercube whose links and nodes fail independently with given probabilities p < 1 and q < 1, respectively. Information held in a fault-free node, called the source, has to reach all other fault-free nodes. Messages may be directly transmitted to adjacent nodes only, and every node may communicate with at most one neighbour in a unit of time. A message can be transmitted only if both communicating neighbours and the link joining them are fault-free. For parameters p and q satisfying (1 – p)(1 – q) ≽ 0.99 (e.g. p = q = 0.5%), we give an algorithm working in time O(log n) and broadcasting source information to all fault-free nodes with probability exceeding 1 – cn-e for some positive constant ε, c depending on p and q but not depending on n.