Refine search
Actions for selected content:
48571 results in Computer Science
CPC volume 4 issue 4 Cover and Front matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Author Index to Volume 1
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. 383-384
-
- Article
- Export citation
Ray C. Dougherty, Natural Language Computing: An English Generative Grammar in Prolog. Hillsdale, NJ: Lawrence Erlbaum. 1994. 349 pages. ISBN 0 8058 1525 2 (hardback), 0 8058 1526 0 (paperback). $69 (hardback), $36 (paperback)
-
- Journal:
- Natural Language Engineering / Volume 1 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 213-215
-
- Article
- Export citation
A Characterisation of Strict Matching Matroids
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 3 / September 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. 209-217
-
- Article
- Export citation
NLE volume 1 issue 4 Cover and Front matter
-
- Journal:
- Natural Language Engineering / Volume 1 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. f1-f2
-
- Article
- Export citation
Analysis of Top To Random Shuffles
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. 135-155
-
- Article
- Export citation
Plane Cubic Graphs with Prescribed Face Areas
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. 371-381
-
- Article
- Export citation
NLE volume 1 issue 4 Cover and Back matter
-
- Journal:
- Natural Language Engineering / Volume 1 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. b1-b6
-
- Article
- Export citation
CPC volume 1 issue 2 Cover and Front matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
CPC volume 2 issue 2 Cover and Front matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Improved Bounds for Mixing Rates of Markov Chains and Multicommodity Flow
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. 351-370
-
- Article
- Export citation
Syntactic Analysis of Hebrew Sentences
-
- Journal:
- Natural Language Engineering / Volume 1 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 261-288
-
- Article
- Export citation
The Numbers of Spanning Trees, Hamilton Cycles and Perfect Matchings in a Random Graph
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. 97-126
-
- Article
- Export citation
A hierarchical Dirichlet language model
-
- Journal:
- Natural Language Engineering / Volume 1 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 289-308
-
- Article
- Export citation
CPC volume 5 issue 4 Cover and Back matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 4 / December 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation
CPC volume 2 issue 3 Cover and Front matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Almost all Berge Graphs are Perfect
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. 53-79
-
- Article
- Export citation
Multivariate Identities, Permutation and Bonferroni Upper Bounds
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 331-342
-
- Article
- Export citation
Cycle Partitions in Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 2 / June 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. 95-97
-
- Article
- Export citation
Image Partition Regularity of Matrices
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. 437-463
-
- Article
- Export citation
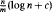 shuffles to get close to random. The formulae lead to new subalgebras in the group algebra of the symmetric group.
shuffles to get close to random. The formulae lead to new subalgebras in the group algebra of the symmetric group.