Refine search
Actions for selected content:
48572 results in Computer Science
A Matroid Reconstruction Result
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. 371-373
-
- Article
- Export citation
NLE volume 1 issue 1 Cover and Front matter
-
- Journal:
- Natural Language Engineering / Volume 1 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. f1-f2
-
- Article
- Export citation
Shortcutting Planar Digraphs*
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 287-315
-
- Article
- Export citation
Precoloring Extension III: Classes of Perfect Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. 35-56
-
- Article
- Export citation
Natural language interfaces to databases – an introduction
-
- Journal:
- Natural Language Engineering / Volume 1 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 29-81
-
- Article
- Export citation
Small Submatroids in Random Matroids
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. 257-266
-
- Article
- Export citation
CPC volume 3 issue 3 Cover and Front matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
A Probabilistic Analysis of a String Editing Problem and its Variations†
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 143-166
-
- Article
- Export citation
On the Number of Convex Lattice Polygons
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. 295-302
-
- Article
- Export citation
On Subgraph Sizes in Random Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. 123-134
-
- Article
- Export citation
On a Random Instance of a ‘Stable Roommates’ Problem: Likely Behavior of the Proposal Algorithm
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. 53-92
-
- Article
- Export citation
NLE volume 1 issue 1 Cover and Back matter
-
- Journal:
- Natural Language Engineering / Volume 1 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. b1-b3
-
- Article
- Export citation
POETIC: A system for gathering and disseminating traffic information†
-
- Journal:
- Natural Language Engineering / Volume 1 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 363-388
-
- Article
- Export citation
On the Thickness of Sparse Random Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 4 / December 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. 303-309
-
- Article
- Export citation
CPC volume 2 issue 1 Cover and Front matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Threshold Functions for H-factors
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. 137-144
-
- Article
- Export citation
Turán-Ramsey Theorems and Kp-Independence Numbers
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 3 / September 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. 297-325
-
- Article
- Export citation
CPC volume 4 issue 2 Cover and Front matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 2 / June 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
The Induced Size-Ramsey Number of Cycles
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 217-239
-
- Article
- Export citation
Natural language processing in an operational clinical information system
-
- Journal:
- Natural Language Engineering / Volume 1 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 83-108
-
- Article
- Export citation
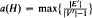 , where the maximum is taken over all subgraphs (
, where the maximum is taken over all subgraphs (