Refine search
Actions for selected content:
48579 results in Computer Science
On Weighted Sequence Sums
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 363-367
-
- Article
- Export citation
Orthogonality of Measures Induced by Random Walks with Scenery
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. 247-256
-
- Article
- Export citation
A Zero-Free Interval for Chromatic Polynomials of Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. 325-336
-
- Article
- Export citation
An Efficient Method of Examining all Trees
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 4 / December 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. 403-413
-
- Article
- Export citation
CPC volume 2 issue 1 Cover and Back matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 12 September 2008, p. b1
-
- Article
-
- You have access
- Export citation
Short Proof of Galvin's Theorem on the List-chromatic Index of a Bipartite Multigraph
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. 91-94
-
- Article
- Export citation
Threshold Channel Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. 337-349
-
- Article
- Export citation
Reliable Broadcasting in Hypercubes with Random Link and Node Failures
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 4 / December 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. 337-350
-
- Article
- Export citation
(1, 2)-Factorizations of General Eulerian Nearly Regular Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 1 / March 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. 87-95
-
- Article
- Export citation
The Self-Avoiding-Walk and Percolation Critical Points in High Dimensions
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 197-215
-
- Article
- Export citation
Components of Random Forests
-
- Journal:
- Combinatorics, Probability and Computing / Volume 1 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 12 September 2008, pp. 35-52
-
- Article
- Export citation
Reconstructing a Graph from its Neighborhood Lists
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 2 / June 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. 103-113
-
- Article
- Export citation
An Introduction to Random Topological Graph Theory
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 4 / December 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. 545-555
-
- Article
- Export citation
Asymptotic Enumeration of Predicate-Junction Flowgraphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 5 / Issue 3 / September 1996
- Published online by Cambridge University Press:
- 12 September 2008, pp. 215-226
-
- Article
- Export citation
CPC volume 3 issue 2 Cover and Back matter
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation
On Vertex-Edge-Critically n-Connected Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 3 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 12 September 2008, pp. 257-271
-
- Article
- Export citation
Optimally Reliable Graphs for Both Vertex and Edge Failures
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 1 / March 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. 93-100
-
- Article
- Export citation
Engineering “word experts” for word disambiguation
-
- Journal:
- Natural Language Engineering / Volume 1 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 339-362
-
- Article
- Export citation
Geometric Approaches to the Estimation of the Spectral Gap of Reversible Markov Chains
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 3 / September 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. 301-323
-
- Article
- Export citation
Ramsey Size Linear Graphs
-
- Journal:
- Combinatorics, Probability and Computing / Volume 2 / Issue 4 / December 1993
- Published online by Cambridge University Press:
- 12 September 2008, pp. 389-399
-
- Article
- Export citation
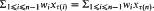
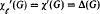 . Here we give a brief self-contained proof of this result.
. Here we give a brief self-contained proof of this result.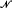 (
(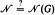 is NP-complete; for bipartite graphs the decision problem is polynomially equivalent to Graph Isomorphism; forests
is NP-complete; for bipartite graphs the decision problem is polynomially equivalent to Graph Isomorphism; forests 