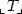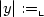Refine search
Actions for selected content:
48532 results in Computer Science
The Critical Phase for Random Graphs with a Given Degree Sequence
-
- Journal:
- Combinatorics, Probability and Computing / Volume 17 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 67-86
-
- Article
- Export citation
Linear tabling strategies and optimizations
-
- Journal:
- Theory and Practice of Logic Programming / Volume 8 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 81-109
-
- Article
- Export citation
The Distribution of Patterns in Random Trees
-
- Journal:
- Combinatorics, Probability and Computing / Volume 17 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 21-59
-
- Article
- Export citation
Tree inclusion problems
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 42 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 18 January 2008, pp. 5-20
- Print publication:
- January 2008
-
- Article
- Export citation
Ethem Alpaydin. Introduction to Machine Learning (Adaptive Computation and Machine Learning Series). The MIT Press, 2004. ISBN: 0 262 01211 1 Price £32.95 / $50.00 (hardcover). xxx+415 pages.
-
- Journal:
- Natural Language Engineering / Volume 14 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 133-137
-
- Article
- Export citation
When is the orbit algebra of a groupan integral domain ? Proof of a conjecture of P.J. Cameron
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 42 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 18 January 2008, pp. 83-103
- Print publication:
- January 2008
-
- Article
- Export citation
The k-Core and Branching Processes
-
- Journal:
- Combinatorics, Probability and Computing / Volume 17 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 111-136
-
- Article
- Export citation
Improving precision of type analysis using non-discriminative union
-
- Journal:
- Theory and Practice of Logic Programming / Volume 8 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 33-79
-
- Article
- Export citation
Balls-in-Bins Processes with Feedback and Brownian Motion
-
- Journal:
- Combinatorics, Probability and Computing / Volume 17 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 87-110
-
- Article
- Export citation
Arithmetization of the field of realswith exponentiation extended abstract
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 42 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 18 January 2008, pp. 105-119
- Print publication:
- January 2008
-
- Article
- Export citation
A complete characterization of primitive recursive intensionalbehaviours
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 42 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 18 January 2008, pp. 69-82
- Print publication:
- January 2008
-
- Article
- Export citation
Exemples de classes d'automates cellulaires
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 42 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 18 January 2008, pp. 37-53
- Print publication:
- January 2008
-
- Article
- Export citation
Rayner Manny, Ann Hockey Beth, Bouillon Pierrette, Putting Linguistics into Speech Recognition. The Regulus Grammar Compiler. With contributions by Nikos Chatzichrisafis, Marianne Santaholma & Marianne Starlander. Foreword by Aravind K. Joshi. Appeared in the series CSLI Studies in Computational Linguistics (series edited by Ann Copestake). Stanford, California, CSLI. ISBN 1-57586-526-2 (paperback), xiv+305 pages. Price: US$25.00, £17.99.
-
- Journal:
- Natural Language Engineering / Volume 14 / Issue 1 / January 2008
- Published online by Cambridge University Press:
- 01 January 2008, pp. 137-140
-
- Article
- Export citation
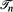 denote the set of unrooted labelled trees of size
denote the set of unrooted labelled trees of size 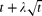 balls (for constant λ∈ℝ), the probability that it always or eventually leads has a non-trivial limit depending on λ.
balls (for constant λ∈ℝ), the probability that it always or eventually leads has a non-trivial limit depending on λ.