Refine search
Actions for selected content:
48462 results in Computer Science
Graphs with Large Girth Not Embeddable in the Sphere
-
- Journal:
- Combinatorics, Probability and Computing / Volume 16 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 829-832
-
- Article
- Export citation
Distance Hereditary Graphs and the Interlace Polynomial
-
- Journal:
- Combinatorics, Probability and Computing / Volume 16 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 947-973
-
- Article
- Export citation
PALS: Efficient Or-Parallel execution of Prolog on Beowulf clusters
-
- Journal:
- Theory and Practice of Logic Programming / Volume 7 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 633-695
-
- Article
- Export citation
FRACTAL AND RESISTANCE DIMENSIONS OF RANDOM TREES
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 21 / Issue 4 / October 2007
- Published online by Cambridge University Press:
- 22 October 2007, pp. 623-634
-
- Article
- Export citation
DYNAMIC ASSIGNMENT OF DEDICATED AND FLEXIBLE SERVERS IN TANDEM LINES
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 21 / Issue 4 / October 2007
- Published online by Cambridge University Press:
- 22 October 2007, pp. 497-538
-
- Article
- Export citation
A STORAGE SYSTEM WITH SPORADIC AND CONTINUOUS CLEARINGS
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 21 / Issue 4 / October 2007
- Published online by Cambridge University Press:
- 22 October 2007, pp. 539-549
-
- Article
- Export citation
SEMI-MARKOV DECISION PROCESSES: NONSTANDARD CRITERIA
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 21 / Issue 4 / October 2007
- Published online by Cambridge University Press:
- 22 October 2007, pp. 635-657
-
- Article
- Export citation
STOCHASTIC COMPARISONS OF PARALLEL SYSTEMS WHEN COMPONENTS HAVE PROPORTIONAL HAZARD RATES
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 21 / Issue 4 / October 2007
- Published online by Cambridge University Press:
- 22 October 2007, pp. 597-609
-
- Article
- Export citation
A MEAN–VARIANCE BOUND FOR A THREE-PIECE LINEAR FUNCTION
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 21 / Issue 4 / October 2007
- Published online by Cambridge University Press:
- 22 October 2007, pp. 611-621
-
- Article
- Export citation
STOCHASTIC BATCH SCHEDULING AND THE “SMALLEST VARIANCE FIRST” RULE
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 21 / Issue 4 / October 2007
- Published online by Cambridge University Press:
- 22 October 2007, pp. 579-595
-
- Article
- Export citation
NONNEGATIVITY OF COVARIANCES BETWEEN FUNCTIONS OF ORDERED RANDOM VARIABLES
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 21 / Issue 4 / October 2007
- Published online by Cambridge University Press:
- 22 October 2007, pp. 557-577
-
- Article
- Export citation
A BAYESIAN APPROACH TO FIND RANDOM-TIME PROBABILITIES FROM EMBEDDED MARKOV CHAIN PROBABILITIES
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 21 / Issue 4 / October 2007
- Published online by Cambridge University Press:
- 22 October 2007, pp. 551-556
-
- Article
- Export citation
Dynamic rebinding for marshalling and update, via redex-time and destruct-time reduction
- Part of
-
- Journal:
- Journal of Functional Programming / Volume 18 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 17 October 2007, pp. 437-502
-
- Article
-
- You have access
- Export citation
On categorical models of classical logic and the Geometry of Interaction
-
- Journal:
- Mathematical Structures in Computer Science / Volume 17 / Issue 5 / October 2007
- Published online by Cambridge University Press:
- 01 October 2007, pp. 957-1027
-
- Article
- Export citation
An algebraic semantics of event-based architectures
-
- Journal:
- Mathematical Structures in Computer Science / Volume 17 / Issue 5 / October 2007
- Published online by Cambridge University Press:
- 01 October 2007, pp. 1029-1073
-
- Article
- Export citation
On the ubiquity of certain total type structures
-
- Journal:
- Mathematical Structures in Computer Science / Volume 17 / Issue 5 / October 2007
- Published online by Cambridge University Press:
- 01 October 2007, pp. 841-953
-
- Article
- Export citation
Behavioural reasoning for conditional equations†
-
- Journal:
- Mathematical Structures in Computer Science / Volume 17 / Issue 5 / October 2007
- Published online by Cambridge University Press:
- 01 October 2007, pp. 1075-1113
-
- Article
- Export citation
Preface
-
- Journal:
- Mathematical Structures in Computer Science / Volume 17 / Issue 5 / October 2007
- Published online by Cambridge University Press:
- 01 October 2007, p. 839
-
- Article
- Export citation
Parallel approximation to high multiplicity scheduling problems VIA smooth multi-valued quadratic programming
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 42 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 25 September 2007, pp. 237-252
- Print publication:
- April 2008
-
- Article
- Export citation
Learning tree languages from text
-
- Journal:
- RAIRO - Theoretical Informatics and Applications / Volume 41 / Issue 4 / October 2007
- Published online by Cambridge University Press:
- 25 September 2007, pp. 351-374
- Print publication:
- October 2007
-
- Article
- Export citation
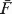
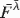
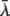
 leads in practice to a relatively small handful of distinct type structures. Among these are the type structure C of Kleene–Kreisel
leads in practice to a relatively small handful of distinct type structures. Among these are the type structure C of Kleene–Kreisel 