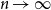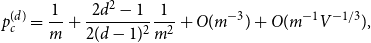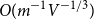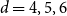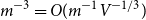Refine search
Actions for selected content:
48229 results in Computer Science
CUT ELIMINATION IN HYPERSEQUENT CALCULUS FOR SOME LOGICS OF LINEAR TIME
-
- Journal:
- The Review of Symbolic Logic / Volume 12 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 13 August 2019, pp. 806-822
- Print publication:
- December 2019
-
- Article
- Export citation

Artificial Intelligence
- Foundations of Computational Agents
-
- Published online:
- 12 August 2019
- Print publication:
- 25 September 2017
-
- Book
- Export citation
Action-Centered Information Retrieval
-
- Journal:
- Theory and Practice of Logic Programming / Volume 20 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 09 August 2019, pp. 249-272
-
- Article
- Export citation
ROB volume 37 issue 9 Cover and Front matter
-
- Article
-
- You have access
- Export citation
ROB volume 37 issue 9 Cover and Back matter
-
- Article
-
- You have access
- Export citation
Assessing the computational complexity of multilayer subgraph detection
-
- Journal:
- Network Science / Volume 7 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 05 August 2019, pp. 215-241
-
- Article
- Export citation
Understanding node-link and matrix visualizations of networks: A large-scale online experiment
-
- Journal:
- Network Science / Volume 7 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 05 August 2019, pp. 242-264
-
- Article
- Export citation
Influence of measurement errors on networks: Estimating the robustness of centrality measures
-
- Journal:
- Network Science / Volume 7 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 05 August 2019, pp. 180-195
-
- Article
-
- You have access
- Open access
- Export citation
A paradigm for longitudinal complex network analysis over patient cohorts in neuroscience
-
- Journal:
- Network Science / Volume 7 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 05 August 2019, pp. 196-214
-
- Article
- Export citation
Designing profitable joint product–service channels: case study on tablet and eBook markets
-
- Journal:
- Design Science / Volume 5 / 2019
- Published online by Cambridge University Press:
- 05 August 2019, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NWS volume 7 issue 2 Cover and Back matter
-
- Journal:
- Network Science / Volume 7 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 05 August 2019, pp. b1-b4
-
- Article
-
- You have access
- Export citation
NWS volume 7 issue 2 Cover and Front matter
-
- Journal:
- Network Science / Volume 7 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 05 August 2019, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Rank monotonicity in centrality measures—Corrigendum
-
- Journal:
- Network Science / Volume 7 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 05 August 2019, pp. 265-268
-
- Article
-
- You have access
- Export citation
Expansion of Percolation Critical Points for Hamming Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 05 August 2019, pp. 68-100
-
- Article
- Export citation
Automatic landmark discovery for learning agents under partial observability
-
- Journal:
- The Knowledge Engineering Review / Volume 34 / 2019
- Published online by Cambridge University Press:
- 02 August 2019, e11
-
- Article
- Export citation
THE LARGE STRUCTURES OF GROTHENDIECK FOUNDED ON FINITE-ORDER ARITHMETIC
-
- Journal:
- The Review of Symbolic Logic / Volume 13 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 02 August 2019, pp. 296-325
- Print publication:
- June 2020
-
- Article
- Export citation
2 - Monoidal Finite-State Automata
- from Part I - Formal Background
-
- Book:
- Finite-State Techniques
- Published online:
- 29 July 2019
- Print publication:
- 01 August 2019, pp 23-42
-
- Chapter
- Export citation
1 - Formal Preliminaries
- from Part I - Formal Background
-
- Book:
- Finite-State Techniques
- Published online:
- 29 July 2019
- Print publication:
- 01 August 2019, pp 3-22
-
- Chapter
- Export citation
Part II - From Theory to Practice
-
- Book:
- Finite-State Techniques
- Published online:
- 29 July 2019
- Print publication:
- 01 August 2019, pp 159-160
-
- Chapter
- Export citation