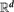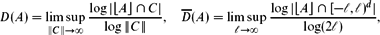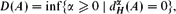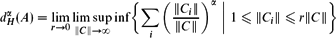Refine search
Actions for selected content:
48167 results in Computer Science
Network patterns of legislative collaboration in twenty parliaments
-
- Journal:
- Network Science / Volume 4 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 24 March 2016, pp. 266-271
-
- Article
- Export citation
Part Four - Biology, Mind, and the Outer Reaches of Quantum Computation
-
- Book:
- The Once and Future Turing
- Published online:
- 05 March 2016
- Print publication:
- 24 March 2016, pp 160-162
-
- Chapter
- Export citation
4 - Cryptography and Computation after Turing
- from Part One - Inside Our Computable World, and the Mathematics of Universality
-
-
- Book:
- The Once and Future Turing
- Published online:
- 05 March 2016
- Print publication:
- 24 March 2016, pp 53-77
-
- Chapter
- Export citation
15 - On Attempting to Model the Mathematical Mind
- from Part Five - Oracles, Infinitary Computation, and the Physics of the Mind
-
-
- Book:
- The Once and Future Turing
- Published online:
- 05 March 2016
- Print publication:
- 24 March 2016, pp 361-378
-
- Chapter
- Export citation
Part Two - The Computation of Processes, and Not Computing the Brain
-
- Book:
- The Once and Future Turing
- Published online:
- 05 March 2016
- Print publication:
- 24 March 2016, pp 90-91
-
- Chapter
- Export citation
Part Three - The Reverse Engineering Road to Computing Life
-
- Book:
- The Once and Future Turing
- Published online:
- 05 March 2016
- Print publication:
- 24 March 2016, pp 129-130
-
- Chapter
- Export citation
13 - Turing's ‘Oracle’: From Absolute to Relative Computability and Back
- from Part Five - Oracles, Infinitary Computation, and the Physics of the Mind
-
-
- Book:
- The Once and Future Turing
- Published online:
- 05 March 2016
- Print publication:
- 24 March 2016, pp 300-334
-
- Chapter
- Export citation
3 - Turing and the Primes
- from Part One - Inside Our Computable World, and the Mathematics of Universality
-
-
- Book:
- The Once and Future Turing
- Published online:
- 05 March 2016
- Print publication:
- 24 March 2016, pp 34-52
-
- Chapter
- Export citation
9 - Turing's Theory of Developmental Pattern Formation
- from Part Three - The Reverse Engineering Road to Computing Life
-
-
- Book:
- The Once and Future Turing
- Published online:
- 05 March 2016
- Print publication:
- 24 March 2016, pp 131-143
-
- Chapter
- Export citation
NWS volume 4 issue 1 Cover and Back matter
-
- Journal:
- Network Science / Volume 4 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 23 March 2016, pp. b1-b5
-
- Article
-
- You have access
- Export citation
Homophily, influence and the decay of segregation in self-organizing networks
-
- Journal:
- Network Science / Volume 4 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 23 March 2016, pp. 81-116
-
- Article
-
- You have access
- Export citation
NWS volume 4 issue 1 Cover and Front matter
-
- Journal:
- Network Science / Volume 4 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 23 March 2016, pp. f1-f3
-
- Article
-
- You have access
- Export citation
INTUITIONISTIC EPISTEMIC LOGIC
-
- Journal:
- The Review of Symbolic Logic / Volume 9 / Issue 2 / June 2016
- Published online by Cambridge University Press:
- 21 March 2016, pp. 266-298
- Print publication:
- June 2016
-
- Article
- Export citation
Multivariate Eulerian Polynomials and Exclusion Processes
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 18 March 2016, pp. 486-499
-
- Article
- Export citation
Classifying sanctions and designing a conceptual sanctioning process model for socio-technical systems
-
- Journal:
- The Knowledge Engineering Review / Volume 31 / Issue 2 / March 2016
- Published online by Cambridge University Press:
- 17 March 2016, pp. 142-166
-
- Article
- Export citation
A language for hierarchical data parallel design-space exploration on GPUs
- Part of
-
- Journal:
- Journal of Functional Programming / Volume 26 / 2016
- Published online by Cambridge University Press:
- 17 March 2016, e6
-
- Article
-
- You have access
- Export citation
Transparent fault tolerance for scalable functional computation
- Part of
-
- Journal:
- Journal of Functional Programming / Volume 26 / 2016
- Published online by Cambridge University Press:
- 17 March 2016, e5
-
- Article
-
- You have access
- Export citation
Marstrand-type Theorems for the Counting and Mass Dimensions in ℤ
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 5 / September 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 700-743
-
- Article
- Export citation
Programming in logic without logic programming
-
- Journal:
- Theory and Practice of Logic Programming / Volume 16 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 269-295
-
- Article
- Export citation