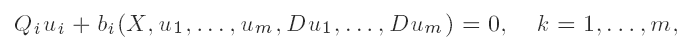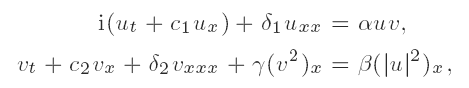Refine search
Actions for selected content:
25847 results in Abstract analysis
20 - Invariant subspaces for commuting contractions
-
- Book:
- Introduction to Banach Algebras, Operators, and Harmonic Analysis
- Published online:
- 29 December 2009
- Print publication:
- 13 November 2003, pp 186-198
-
- Chapter
- Export citation
26 - Semi-regular operators
-
- Book:
- Introduction to Banach Algebras, Operators, and Harmonic Analysis
- Published online:
- 29 December 2009
- Print publication:
- 13 November 2003, pp 267-284
-
- Chapter
- Export citation
2 - Ideals and the spectrum
-
- Book:
- Introduction to Banach Algebras, Operators, and Harmonic Analysis
- Published online:
- 29 December 2009
- Print publication:
- 13 November 2003, pp 12-19
-
- Chapter
- Export citation
24 - Preservation of spectra and index
-
- Book:
- Introduction to Banach Algebras, Operators, and Harmonic Analysis
- Published online:
- 29 December 2009
- Print publication:
- 13 November 2003, pp 230-240
-
- Chapter
- Export citation
Estimates for the three-wave interaction of surface water waves
-
- Journal:
- European Journal of Applied Mathematics / Volume 14 / Issue 5 / October 2003
- Published online by Cambridge University Press:
- 24 October 2003, pp. 547-570
-
- Article
- Export citation
Transport equations with resting phases
-
- Journal:
- European Journal of Applied Mathematics / Volume 14 / Issue 5 / October 2003
- Published online by Cambridge University Press:
- 24 October 2003, pp. 613-636
-
- Article
- Export citation
An $n$-populations model for traffic flow
-
- Journal:
- European Journal of Applied Mathematics / Volume 14 / Issue 5 / October 2003
- Published online by Cambridge University Press:
- 24 October 2003, pp. 587-612
-
- Article
- Export citation
ERRATUM
-
- Journal:
- European Journal of Applied Mathematics / Volume 14 / Issue 5 / October 2003
- Published online by Cambridge University Press:
- 24 October 2003, p. 637
-
- Article
- Export citation
An Eigenvalue problem for holomorphic solutions to a certain class of functional differential equations
-
- Journal:
- European Journal of Applied Mathematics / Volume 14 / Issue 5 / October 2003
- Published online by Cambridge University Press:
- 24 October 2003, pp. 571-585
-
- Article
- Export citation
Reduced wave Green's functions and their effect on the dynamics of a spike for the Gierer–Meinhardt model
-
- Journal:
- European Journal of Applied Mathematics / Volume 14 / Issue 5 / October 2003
- Published online by Cambridge University Press:
- 24 October 2003, pp. 513-545
-
- Article
- Export citation
Phragmén–Lindelöf theorems in slabs for some systems of non-hyperbolic second-order quasi-linear equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 133 / Issue 5 / October 2003
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1155-1173
- Print publication:
- October 2003
-
- Article
- Export citation
Axial symmetry of solutions to semilinear elliptic equations in unbounded domains
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 133 / Issue 5 / October 2003
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1175-1192
- Print publication:
- October 2003
-
- Article
- Export citation
Set products in transformation semigroups
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 133 / Issue 5 / October 2003
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1121-1135
- Print publication:
- October 2003
-
- Article
- Export citation
Non-stabilizing solutions of semilinear hyperbolic and elliptic equations with damping
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 133 / Issue 5 / October 2003
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1137-1153
- Print publication:
- October 2003
-
- Article
- Export citation
Weak solutions for equations defined by accretive operators. I
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 133 / Issue 5 / October 2003
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1193-1207
- Print publication:
- October 2003
-
- Article
- Export citation
Existence and stability of ground-state solutions of a Schrödinger—KdV system
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 133 / Issue 5 / October 2003
- Published online by Cambridge University Press:
- 12 July 2007, pp. 987-1029
- Print publication:
- October 2003
-
- Article
- Export citation
Stability of some unilateral free-discontinuity problems in two-dimensional domains
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 133 / Issue 5 / October 2003
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1031-1046
- Print publication:
- October 2003
-
- Article
- Export citation
Boundedness and asymptotic stability for delayed equations of logistic type
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 133 / Issue 5 / October 2003
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1057-1073
- Print publication:
- October 2003
-
- Article
- Export citation
Conormal morphisms
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 133 / Issue 5 / October 2003
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1047-1056
- Print publication:
- October 2003
-
- Article
- Export citation
Saint-Venant's principle in blow-up for higher-order quasilinear parabolic equations
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 133 / Issue 5 / October 2003
- Published online by Cambridge University Press:
- 12 July 2007, pp. 1075-1119
- Print publication:
- October 2003
-
- Article
- Export citation